参考：

本文主要讨论流体力学基本方程（ Navier-Stokes 方程）的推导。

读者可能会对计算流体力学基本方程的各种各样的形式感到困惑，从而产生距离、产生抗拒。下文将反复推导公式，一方面让读者理解方程的由来，另一方面也是让读者能够“理直气壮”。以后遇到这些方程或者这些方程的变化，不再陌生抗拒，可以在心中点评一句“嗯~确实如此”。

先作几个简单的说明，

  • 定常是指流动性质不随时间变化，反之为非定常
  • 可压是指密度不为常数，反之为不可压
  • 我们一般研究牛顿流体较多，也从牛顿流体开始讨论
  • 暂不讨论偏微分方程的双曲、椭圆、抛物数学性质
  • 流体分子 ∈\in 流体质点 ∈\in 流体微团 ∈\in 流体系统（控制体或物质体）
    • 流体微团宏观上足够小（使用离散方法），微观上足够大（仍为连续介质）

经典力学中会通过运动方程等数学公式来描述一个物体的状态。那么，流体的状态怎么描述呢？

手推公式非常重要！请手推两遍以上。
手推公式非常重要！请手推两遍以上。
手推公式非常重要！请手推两遍以上。

讨论前

一些约定和表示

为了方便书写，本系列除非特别说明，大写字母一般表示物理量的矢量。

速度矢量

U=(u1u2u3)U = \begin{pmatrix}u_{1} \\ u_{2} \\ u_{3}\end{pmatrix}

速度对时间的偏导

∂U∂t=(∂u1∂t,∂u2∂t,∂u3∂t)T\frac{\partial U}{\partial t} = \bigg(\frac{\partial u_{1}}{\partial t} , \frac{\partial u_{2}}{\partial t} , \frac{\partial u_{3}}{\partial t} \bigg)^{T}

∇\nabla （\nabla）算子

∇=(∂∂x,∂∂y,∂∂z)T\nabla = \bigg( \frac{\partial }{\partial x},\frac{\partial }{\partial y}, \frac{\partial }{\partial z} \bigg)^{T}

拉普拉算子 ∇2\nabla^{2}

∇⋅(∇U)=∇2U\nabla\cdot(\nabla U) = \nabla^{2}U

速度的梯度（空间梯度）（梯度升维）

∇U=[∂u1∂x∂u2∂x∂u3∂x∂u1∂y∂u2∂y∂u3∂y∂u1∂z∂u2∂z∂u3∂z]\nabla U = \begin{bmatrix} \frac{\partial u_{1}}{\partial x} & \frac{\partial u_{2}}{\partial x} & \frac{\partial u_{3}}{\partial x} \\ \frac{\partial u_{1}}{\partial y} & \frac{\partial u_{2}}{\partial y} & \frac{\partial u_{3}}{\partial y} \\ \frac{\partial u_{1}}{\partial z} & \frac{\partial u_{2}}{\partial z} & \frac{\partial u_{3}}{\partial z} \end{bmatrix}

速度的散度（散度降维）

∇⋅U=∂u1∂x+∂u2∂y+∂u3∂z\nabla\cdot U = \frac{\partial u_{1}}{\partial x} + \frac{\partial u_{2}}{\partial y} + \frac{\partial u_{3}}{\partial z}

速度梯度的散度

∇⋅(∇U)=∇2U=∇⋅[∂u1∂x∂u2∂x∂u3∂x∂u1∂y∂u2∂y∂u3∂y∂u1∂z∂u2∂z∂u3∂z]=[∂∂x(∂u1∂x)+∂∂y(∂u1∂y)+∂∂z(∂u1∂z)∂∂x(∂u2∂x)+∂∂y(∂u2∂y)+∂∂z(∂u2∂z)∂∂x(∂u3∂x)+∂∂y(∂u3∂y)+∂∂z(∂u3∂z)]\nabla\cdot(\nabla U) = \nabla^{2}U = \nabla\cdot \begin{bmatrix} \frac{\partial u_{1}}{\partial x} & \frac{\partial u_{2}}{\partial x} & \frac{\partial u_{3}}{\partial x} \\ \frac{\partial u_{1}}{\partial y} & \frac{\partial u_{2}}{\partial y} & \frac{\partial u_{3}}{\partial y} \\ \frac{\partial u_{1}}{\partial z} & \frac{\partial u_{2}}{\partial z} & \frac{\partial u_{3}}{\partial z} \end{bmatrix} = \begin{bmatrix} \frac{\partial}{\partial x}\left(\frac{\partial u_{1}}{\partial x}\right) + \frac{\partial}{\partial y}\left(\frac{\partial u_{1}}{\partial y}\right)+ \frac{\partial}{\partial z}\left(\frac{\partial u_{1}}{\partial z}\right) \\ \frac{\partial}{\partial x}\left(\frac{\partial u_{2}}{\partial x}\right) + \frac{\partial}{\partial y}\left(\frac{\partial u_{2}}{\partial y}\right)+ \frac{\partial}{\partial z}\left(\frac{\partial u_{2}}{\partial z}\right) \\ \frac{\partial}{\partial x}\left(\frac{\partial u_{3}}{\partial x}\right) + \frac{\partial}{\partial y}\left(\frac{\partial u_{3}}{\partial y}\right)+ \frac{\partial}{\partial z}\left(\frac{\partial u_{3}}{\partial z}\right) \\ \end{bmatrix}

速度和 ∇\nabla 算子的内积（对流导数）

U⋅∇=u1∂∂x+u2∂∂y+u3∂∂zU\cdot\nabla = u_{1}\frac{\partial }{\partial x} + u_{2}\frac{\partial }{\partial y} + u_{3}\frac{\partial }{\partial z}

速度的对流导数

(U⋅∇)U=[u1∂u1∂x+u2∂u1∂y+u3∂u1∂zu1∂u2∂x+u2∂u2∂y+u3∂u2∂zu1∂u3∂x+u2∂u3∂y+u3∂u3∂z](U\cdot\nabla)U= \begin{bmatrix} u_{1}\frac{\partial u_{1}}{\partial x} + u_{2}\frac{\partial u_{1}}{\partial y} + u_{3}\frac{\partial u_{1}}{\partial z} \\ u_{1}\frac{\partial u_{2}}{\partial x} + u_{2}\frac{\partial u_{2}}{\partial y} + u_{3}\frac{\partial u_{2}}{\partial z} \\ u_{1}\frac{\partial u_{3}}{\partial x} + u_{2}\frac{\partial u_{3}}{\partial y} + u_{3}\frac{\partial u_{3}}{\partial z} \\ \end{bmatrix}

拉格朗日和欧拉

对于流体力学来说，跟踪研究特定的流体微团的运动的方法就是拉格朗日法。很多数情况下，我们也许只想了解某个流场的信息而不是某些流体微团的信息。研究某一个流体区域而不是跟踪特定流体微团的方法就是欧拉法。

  • 基于拉格朗日法，选取的跟踪研究的流体微团的集合体被称为“物质体”（material volume, MV）
    • 物质体所包含的流体微团数量固定，即质量固定
    • 物质体的体积可能变化
    • 物质体微元仍包含一定的流体分子
  • 基于欧拉法，选取的研究区域被称为“控制体”（control volume, CV）
    • 控制体所包含的物质可能变化，即质量可能变化
    • 控制体的体积固定
    • 控制体微元仍包含若干流体分子

例如，对于拉格朗日法来说，对于物质体，其中有流体微团 a，它的速度描述为 U(xa,ya,za,t)U(x_a, y_a, z_a, t) ，空间参数就是跟踪的对象 a 的坐标，物质体中每个流体微团都需要各自的坐标。对于欧拉法来说，对于控制体，它的速度描述为 U(x,y,z,t)U(x, y, z, t) ，空间参数是控制体空间中的任意点的坐标，当我们给定一组空间参数的时候，表示控制体中该时刻经过该位置的流体微团的速度，下一时刻这个位置上可能就是别的流体微团了。

物质体和控制体的定义在本文讨论中非常重要。

注意时刻区别两种方式，能够更加深刻理解基本方程的推导和各种形式间联系。后文遇到“物质体”和“控制体”时，如果感觉模糊，可以反复回到这里，理解体积和质量变化的不同。

基于两种描述方法的微妙不同，下面我们先讨论几个重要概念。

通量

数学上，速度 UfU_{f} （在经过该面的速度矢量）乘以面积 SfS_{f} （面矢量）就是体积通量，表示单位时间流过某个面积的流体流体，即

ϕf=Uf⋅Sf\phi_{f} = U_{f}\cdot S_{f}

相应的，质量通量有

ρfUf⋅Sf\rho_{f}U_{f}\cdot S_{f}

考虑单位时间单位面积的体积通量，即

Uf⋅Sf∣Sf∣=Uf⋅nfU_{f}\cdot \frac{S_{f}}{|S_{f}|} = U_{f}\cdot n_{f}

其中，nfn_{f} 称为面单位法向矢量，用于定义面的法向方向。

考虑如果速度矢量和面法向有夹角 θ\theta （单元中心速度和面法向不一致），则需要考虑非正交性，此时的体积通量为

ϕf=Uf⋅Sf=∣Uf∣∣Sf∣cosθ\phi_{f} = U_{f}\cdot S_{f} = |U_{f}||S_{f}|cos\theta

广义上来说，UfU_{f} 和 ρfUf\rho_{f} U_{f} 都被称为对流通量，后面会介绍扩散通量的定义。

在有限体积法的讨论中，我们会逐渐理会到，守恒很多时候在本质上体现为通量的守恒。

速度散度

对于一个物质体的微元来说，体积是可能发生变化的。

物质体的微元上一个无穷小的面单元，它运动后产生的体积变化为（体积 = 速度×时间×底面积）

ΔV=[(U⃗Δt)⋅n⃗]ds=(U⃗Δt)⋅dS⃗\Delta V = [(\vec U \Delta t) \cdot \vec n] ds = (\vec U \Delta t) \cdot d\vec S

细究的话，这里其实是有一个微分近似，因为物质体的微元非常小，所以不考虑相对速度，面单元的速度约等于物质体的速度 U⃗\vec U。

速度 U⃗\vec U 是物质体的微元的速度而不是物质体内流体微团的函数。虽然 U⃗\vec U 是空间和时间的函数，但是时间变化是极短的，所以速度随时间的变化也是极小的，也就是说，这个极小的时间变化内，速度近似的与时间独立，所以速度 U⃗\vec U 可以直接乘以时间步 Δt\Delta t 。

物质体整个体积变化需要在微元整个面上作积分，为

∬S(U⃗Δt)⋅dS⃗\iint_S(\vec U \Delta t) \cdot d\vec S

体积变化对时间的变化率为

dVdt≈1Δt∬S(U⃗Δt)⋅dS⃗=∬SU⃗⋅dS⃗\frac{dV}{dt} \approx \frac{1}{\Delta t}\iint_S(\vec U \Delta t) \cdot d\vec S = \iint_S \vec U \cdot d \vec S

因为近似认为速度在时间 Δt\Delta t 上变化极小，所以 Δt\Delta t 与速度独立，单独拿到外面约去。

由散度定理，物理量的面积分等于其散度的体积分。上式的面积分转化为体积分，

dVdt=∭V(∇⋅U⃗)dV\frac{dV}{dt} = \iiint_V(\nabla \cdot \vec U) dV

如果这个物质体的体积十分微小，取为 δV\delta V

d(δV)dt=∭δV(∇⋅U⃗)dV\frac{d(\delta V)}{dt} = \iiint_{\delta V}(\nabla \cdot \vec U) dV

微小体积的体积分约等于直接乘以这个微小体积，而速度仍然这个微小体积的速度。

d(δV)dt=(∇⋅U⃗)δV\frac{d(\delta V)}{dt} = (\nabla \cdot \vec U) \delta V

最终可得

∇⋅U⃗=1δVd(δV)dt\nabla \cdot \vec U = \frac{1}{\delta V}\frac{d(\delta V)}{dt}

注意哈密顿算子其实是一个矢量，点乘一个速度矢量之后，得到一个标量。

∇⋅U⃗=∂u∂x+∂v∂y+∂w∂z\nabla \cdot \vec U = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z}

速度的散度就是单位时间单位体积的流体微团的体积变化。

下文将多次遇到这一项。

我们停下脚步，考虑一下上面的讨论。

体积的变化是从物质体的微元的面单元开始的。当我们取一个控制体，这个控制体和物质体微元的初始状态一模一样。物质体的面单元的运动产生体积变化，对于控制体来说，就是“体积”的进出变化。

从上面推导的结果来看，“体积”的流入流出就是速度散度的物理意义。需要意识到，体积流入流出的背后其实是“质量通量”，以后在推导有限体积法的时候会看到。

那么其他物理量的流入流出呢？

散度体现了一个系统的流入流出变化。当散度大于零，意味着系统流出大于流入，系统处于“膨胀”状态。当散度小于零，意味着系统流出小于流入，系统处于“收缩”状态。

我们另外有拉普拉斯算符，定义如下

标量的拉普拉斯计算为

∇⋅(∇s)=∇2s=∂2s∂x2+∂2s∂y2+∂2s∂z2\nabla \cdot (\nabla s) = \nabla^2s = \frac{\partial^2 s}{\partial x^2} + \frac{\partial^2 s}{\partial y^2} + \frac{\partial^2 s}{\partial z^2}

矢量的拉普拉斯计算为

∇2U⃗=(∇2u)i⃗+(∇2v)j⃗+(∇2w)k⃗\nabla^2 \vec U = (\nabla^2u)\vec i + (\nabla^2v)\vec j + (\nabla^2w)\vec k

物质导数

物质导数某种程度上联系了拉格朗日法和欧拉法

我们描述一个非稳态（也就是随时间变化的）流动。拉格朗日描述下，取一个物质体，某个时刻，物质体中某个流体微团的速度和密度如下（分量形式），

{u=u(x,y,z,t)v=v(x,y,z,t)w=w(x,y,z,t)ρ=ρ(x,y,z,t)\begin{cases} u = u(x, y , z, t) \\ v = v(x, y, z, t) \\ w = w(x, y, z, t) \\ \rho = \rho(x, y, z, t) \end{cases}

在时间 t1t_1 时刻，某个流体微团的位置是 (x1,y1,z1)(x_1, y_1, z_1)

ρ1=ρ(x1,y1,z1,t1)\rho_1 = \rho(x_1, y_1, z_1, t_1)

在时间 t2t_2 时刻，该流体微团运动到位置 (x2,y2,z2)(x_2, y_2, z_2)

ρ2=ρ(x2,y2,z2,t2)\rho_2 = \rho(x_2, y_2, z_2, t_2)

注意这个过程，流体微团本身因为时间推进，自身属性会变化，这部分我们称为本地影响。另一方面，流体单元移动到了不同的位置，当然也会对最终呈现出的属性有影响，我们称为对流影响。

对四个变量，作泰勒展开

ρ2=ρ1+(∂ρ∂x)1(x2−x1)+(∂ρ∂y)1(y2−y1)+(∂ρ∂z)1(z2−z1)+(∂ρ∂t)1(t2−t1)+(higherOrderTerms)\rho_2 = \rho_1 + (\frac{\partial \rho}{\partial x})_1(x_2 - x_1) + (\frac{\partial \rho}{\partial y})_1(y_2 - y_1) + (\frac{\partial \rho}{\partial z})_1(z_2 - z_1) + (\frac{\partial \rho}{\partial t})_1(t_2 - t_1) + (higherOrderTerms)

两边都除以 (t2−t1)(t_2 - t_1)， 忽略高阶项的影响

ρ2−ρ1t2−t1≈(∂ρ∂x)1x2−x1t2−t1+(∂ρ∂y)1y2−y1t2−t1+(∂ρ∂z)1z2−z1t2−t1+(∂ρ∂t)1\frac{\rho_2 - \rho_1}{t_2 - t_1} \approx (\frac{\partial \rho}{\partial x})_1\frac{x_2 - x_1}{t_2 - t_1} + (\frac{\partial \rho}{\partial y})_1\frac{y_2 - y_1}{t_2 - t_1} + (\frac{\partial \rho}{\partial z})_1\frac{z_2 - z_1}{t_2 - t_1} + (\frac{\partial \rho}{\partial t})_1

这个等式就描述了一个流体微团在某个时间步长内空间运动后，密度随时间的变化。

当这个时间步长非常小的时候，有极限

lim⁡t2→t1ρ2−ρ1t2−t1=DρDt\lim_{t_2 \rightarrow t_1} \frac{\rho_2 -\rho_1}{t_2 - t_1} = \frac{D\rho}{Dt}

得到密度对时间的全导数，即物理量对过程中的空间变量和时间变量都是变化的。该导数也被称为拉格朗日导数。

注意比较的是，(∂ρ/∂t)(\partial \rho / \partial t) 描述的是密度仅仅随时间变化，而不涉及空间变化，也被称为欧拉导数。

其他项同样取极限有

lim⁡t2→t1x2−x1t2−t1=ulim⁡t2→t1y2−x1y2−t1=vlim⁡t2→t1z2−x1z2−t1=w\begin{aligned} \lim_{t_2 \rightarrow t_1} \frac{x_2 -x_1}{t_2 - t_1} &= u \\ \lim_{t_2 \rightarrow t_1} \frac{y_2 -x_1}{y_2 - t_1} &= v \\ \lim_{t_2 \rightarrow t_1} \frac{z_2 -x_1}{z_2 - t_1} &= w \end{aligned}

上面的泰勒展开式可以写成

DρDt=u∂ρ∂x+v∂ρ∂y+w∂ρ∂z+∂ρ∂t\frac{D\rho}{Dt} = u\frac{\partial \rho}{\partial x} + v\frac{\partial \rho}{\partial y} + w\frac{\partial \rho}{\partial z} + \frac{\partial \rho}{\partial t}

这个式子推广开对其他物理量也成立，得到物质导数（material substatial）的通用形式

DDt=u∂∂x+v∂∂y+w∂∂z+∂∂t\frac{D}{Dt} = u\frac{\partial}{\partial x} + v\frac{\partial }{\partial y} + w\frac{\partial }{\partial z} + \frac{\partial }{\partial t}

引入哈密顿算子

∇=∂∂xi⃗+∂∂yj⃗+∂∂yk⃗\nabla = \frac{\partial }{\partial x} \vec i + \frac{\partial }{\partial y} \vec j + \frac{\partial }{\partial y} \vec k

最终写成

物质导数

DDt=∂∂t+U⋅∇\frac{D}{Dt} = \frac{\partial }{\partial t} + U \cdot \nabla

  • 为了书写方便，约定使用大写的 UU 表示速度矢量

哈密顿算子和矢量的点乘与普通两个矢量点乘是一样的，但是要注意顺序

所以：

  • D/DtD/Dt 称为物质导数，表示物理量的随时间的完整变化，其实是拉格朗日法的
  • ∂/∂t\partial / \partial t 称为本地导数，表示物理上空间运动过程中的时间变化影响，是欧拉法的
  • U⋅∇U\cdot\nabla 称为对流导数， 表示物理上空间运动过程中的对流变化影响，也是欧拉法的
  • 结合下文对雷诺输运定理的讨论，理解将会更加清晰

下面举例说明物质导数各项的物理意义

对于流体微团的温度，

DTDt=∂T∂t+U⋅∇T=∂T∂t+u∂T∂x+v∂T∂y+w∂T∂z\frac{DT}{Dt} = \frac{\partial T}{\partial t} + U \cdot \nabla T= \frac{\partial T}{\partial t} + u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} + w\frac{\partial T}{\partial z}

对于一个空间上从 P1P_1 移动到 P2P_2 ，时间上 t1t_1 到 t2t_2 的流体单元来说，

  • ∂T/∂t\partial T/ \partial t 无论流体单元怎么移动，它都会固有的因为时间变化而自身温度发生变化
  • U⋅∇TU\cdot\nabla T 因为流体单元在空间移动（“移动”其实不准确，更应该是一种“对流”，“交换”，结合下文雷诺输运定理理解），它的温度发生变化

实际上，物质导数就是数学上全导数应用链式法则的完全展开

对于 ρ(x,y,z,t)\rho(x, y, z, t) 函数，全导数为

dρ=∂ρ∂xdx+∂ρ∂ydy+∂ρ∂zdz+∂ρ∂tdtd\rho = \frac{\partial \rho}{\partial x}dx + \frac{\partial \rho}{\partial y}dy + \frac{\partial \rho}{\partial z}dz + \frac{\partial \rho}{\partial t}dt

整理为

dρdt=∂ρ∂t+∂ρ∂xdxdt+∂ρ∂ydydt+∂ρ∂zdzdt\frac{d\rho}{dt} = \frac{\partial \rho}{\partial t} + \frac{\partial \rho}{\partial x}\frac{dx}{dt} + \frac{\partial \rho}{\partial y}\frac{dy}{dt} + \frac{\partial \rho}{\partial z}\frac{dz}{dt}

上式左侧使用 DD 的话，也就是物质导数。

雷诺输运定理

雷诺输运定理是联系拉格朗日法和欧拉法的另一个表现

上面物质导数的讨论是基于流体微团的，下面讨论对象扩大到物质体（包含固定数量的流体微团，但是外形和位置不一定固定）。

我们假设一个任意物理量 BB ，它的单位质量强度为 bb ，也就是有 b=dB/dmb = dB/dm 。

在 tt 时刻，物质体（黑色线条）和控制体（红色线条）重合，经过 Δt\Delta t 之后，物质体移动到新的位置（蓝色线条）

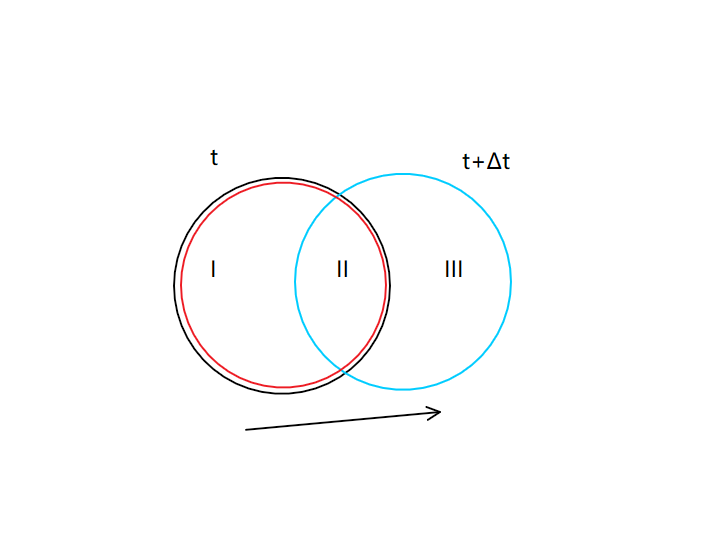
image.png|275

tt 时刻的物质体有

B(t)=BI(t)+BII(t)B(t) = B_I(t) + B_{II}(t)

t+Δtt + \Delta t 时刻的物质体有

B(t+Δt)=BII(t+Δt)+BIII(t+Δt)B(t+\Delta t) = B_{II}(t+\Delta t) + B_{III}(t+\Delta t)

物质体内 BB 的变化如下

(dBdt)MV=lim⁡Δt→0B(t+Δt)−B(t)Δt=lim⁡Δt→0BII(t+Δt)+BIII(t+Δt)−BI(t)−BII(t)Δt=lim⁡Δt→0BI(t+Δt)+BII(t+Δt)−BI(t)−BII(t)Δt+lim⁡Δt→0BIII(t+Δt)Δt−lim⁡Δt→0BI(t+Δt)Δt\begin{aligned} (\frac{dB}{dt})_{MV} &=\lim_{\Delta t \rightarrow 0}\frac{B(t+\Delta t) - B(t)}{\Delta t} \\ &= \lim_{\Delta t \rightarrow 0}\frac{B_{II}(t+\Delta t) +B_{III}(t+\Delta t) - B_I(t) - B_{II}(t)}{\Delta t} \\ &= \lim_{\Delta t \rightarrow 0}\frac{B_{I}(t+\Delta t) + B_{II}(t+\Delta t) - B_I(t) - B_{II}(t)}{\Delta t} \\ &+ \lim_{\Delta t \rightarrow 0}\frac{B_{III}(t+\Delta t)}{\Delta t} - \lim_{\Delta t \rightarrow 0}\frac{B_{I}(t+\Delta t)}{\Delta t} \end{aligned}

上式整理合并后，其中的

lim⁡Δt→0BI(t+Δt)+BII(t+Δt)−BI(t)−BII(t)Δt=lim⁡Δt→0BCV(t+Δt)−BCV(t)Δt=(dBdt)CV\begin{aligned} \lim_{\Delta t \rightarrow 0}\frac{B_{I}(t+\Delta t) + B_{II}(t+\Delta t) - B_I(t) - B_{II}(t)}{\Delta t} &= \lim_{\Delta t \rightarrow 0}\frac{B_{CV}(t+\Delta t) - B_{CV}(t)}{\Delta t} \\ &= (\frac{dB}{dt})_{CV} \end{aligned}

而余下的

lim⁡Δt→0BIII(t+Δt)Δt−lim⁡Δt→0BI(t+Δt)Δt \lim_{\Delta t \rightarrow 0}\frac{B_{III}(t+\Delta t)}{\Delta t} - \lim_{\Delta t \rightarrow 0}\frac{B_{I}(t+\Delta t)}{\Delta t}

两项之差就是通过控制体边界面的 BB 的单位时间净流量。

总结来说就是：

BB 在物质体内的总变化 = BB 在控制体内的变化 + BB 在控制体表面上的净流量

我们约定，为了书写方便，无论是体积分还是面积分，后文大多使用单积分符，即

∬S→∫S\iint_S \rightarrow\int_S

∭V→∫V\iiint_V \rightarrow \int_V

写成数学表达式为

(dBdt)MV=ddt(∫V(t)bρdV)+∫S(t)bρUr⋅n⃗dS(\frac{dB}{dt})_{MV} = \frac{d}{dt}(\int_{V(t)}b\rho dV) + \int_{S(t)}b\rho U_r \cdot \vec n dS

假设流体的流动速度为 U(t,x⃗)U(t, \vec x) ，控制体表面变形的速度为 US(t,x⃗)U_S(t, \vec x) , 流体离开或者进入控制体表面时候的相对速度为 Ur(t,x⃗)=U(t,x⃗)−US(t,x⃗)U_r(t, \vec x) = U(t, \vec x) - U_S(t, \vec x)。

对于一个位置固定的控制体，没有表面变形，即 US=0U_S = 0 ，所以 Ur(t,x⃗)=U(t,x⃗)U_r(t, \vec x) = U(t, \vec x)

虽然体积和面积分别写成 V(t),S(t)V(t),S(t) ，但欧拉描述下控制体的体积和面积不随时间变化。

控制体的几何和时间无关，所以有

ddt(∫VbρdV)=∫V∂∂t(bρ)dV\frac{d}{dt}(\int_V b\rho dV) = \int_V \frac{\partial}{\partial t}(b\rho) dV

代入后有

(dBdt)MV=∫V∂∂t(bρ)dV+∫SbρU⋅n⃗dS(\frac{dB}{dt})_{MV} = \int_V \frac{\partial}{\partial t}(b\rho) dV + \int_{S}b\rho U \cdot \vec n dS

利用散度定理（面积分等于散度的体积分）

(dBdt)MV=∫V∂∂t(bρ)dV+∫SbρU⋅n⃗dS=∫V∂∂t(bρ)dV+∫V∇⋅(ρUb)dV(\frac{dB}{dt})_{MV} = \int_V \frac{\partial}{\partial t}(b\rho) dV + \int_{S}b\rho U \cdot \vec n dS =\int_V \frac{\partial}{\partial t}(b\rho) dV + \int_V \nabla \cdot (\rho U b) dV

整理为

(dBdt)MV=∫V[∂∂t(ρb)+∇⋅(ρUb)]dV(\frac{dB}{dt})_{MV} = \int_V[\frac{\partial}{\partial t}(\rho b) + \nabla \cdot (\rho U b)]dV

散度展开

(dBdt)MV=∫V[∂∂t(ρb)+(ρb∇⋅U+U⋅∇ρb)]dV=∫V[(∂∂t(ρb)+U⋅∇ρb)+ρb∇⋅U]dV\begin{aligned} (\frac{dB}{dt})_{MV} &= \int_V[\frac{\partial}{\partial t}(\rho b) + (\rho b \nabla \cdot U + U \cdot\nabla \rho b)]dV \\ &= \int_V[(\frac{\partial}{\partial t}(\rho b) + U\cdot\nabla \rho b) + \rho b \nabla \cdot U]dV \end{aligned}

利用物质导数，进一步改写为

∫V[(∂∂t(ρb)+U⋅∇ρb)+ρb∇⋅U]dV=∫V[DDt(ρb)+ρb∇⋅U]dV\int_V[(\frac{\partial}{\partial t}(\rho b) + U\cdot\nabla \rho b) + \rho b \nabla \cdot U]dV = \int_V[\frac{D}{D t}(\rho b) + \rho b \nabla \cdot U]dV

最终得到【雷诺输运定理】

(dBdt)MV=∫V[∂∂t(ρb)+∇⋅(ρUb)]dV=∫V[DDt(ρb)+ρb∇⋅U]dV(\frac{dB}{dt})_{MV} = \int_V[\frac{\partial}{\partial t}(\rho b) + \nabla \cdot (\rho U b)]dV = \int_V[\frac{D}{D t}(\rho b) + \rho b \nabla \cdot U]dV

所以也能得到换算关系

DDt(ρb)+ρb∇⋅U=∂∂t(ρb)+∇⋅(ρUb)\frac{D}{D t}(\rho b) + \rho b \nabla \cdot U = \frac{\partial}{\partial t}(\rho b) + \nabla \cdot (\rho U b)

我们姑且称为【雷诺输运换算】。

通过换算讨论，我们再次可以感受到，全导（D/DtD/Dt）是拉格朗日的。

雷诺输运定理显式的表达了物理量在输运过程中的“守恒”。后文将进一步讨论此“守恒”。

质量方程

我们从质量方程（连续性方程）的推导正式开始。

质量守恒

物质体模型

假设我们取一个随着流体流动的物质体，我们可以直接使用物质导数。

这个物质体内部的流体微团数量固定，所以质量固定不变。

物质体的质量为

m=∭VρdVm = \iiint_V \rho dV

质量的物质导数等于零。

DDt∭VρdV=0(1)\frac{D}{Dt}\iiint_V \rho dV = 0 \tag{1}

方程（1）被称为质量方程的非守恒型积分形式

  • 非守恒是因为没有用到守恒关系
  • 积分是因为体积的积分计算
  • 拉格朗日法

注意这里有个坑，方程（1）由物质导数直接展开为下式是错误的

DDt∭VρdV=∭V[∂ρ∂t+U⋅∇ρ]dV=0\cancel{\frac{D}{Dt}\iiint_V \rho dV = \iiint_V [\frac{\partial \rho}{\partial t} + U \cdot \nabla \rho]dV= 0}

在下文换算关系中将讨论此问题

控制体模型

假设我们取一个固定的控制体，我们可以建立守恒关系

单位时间内通过控制体表面流出的质量流量 = 单位时间内控制体内流体的质量减少

B=CB = C

|425

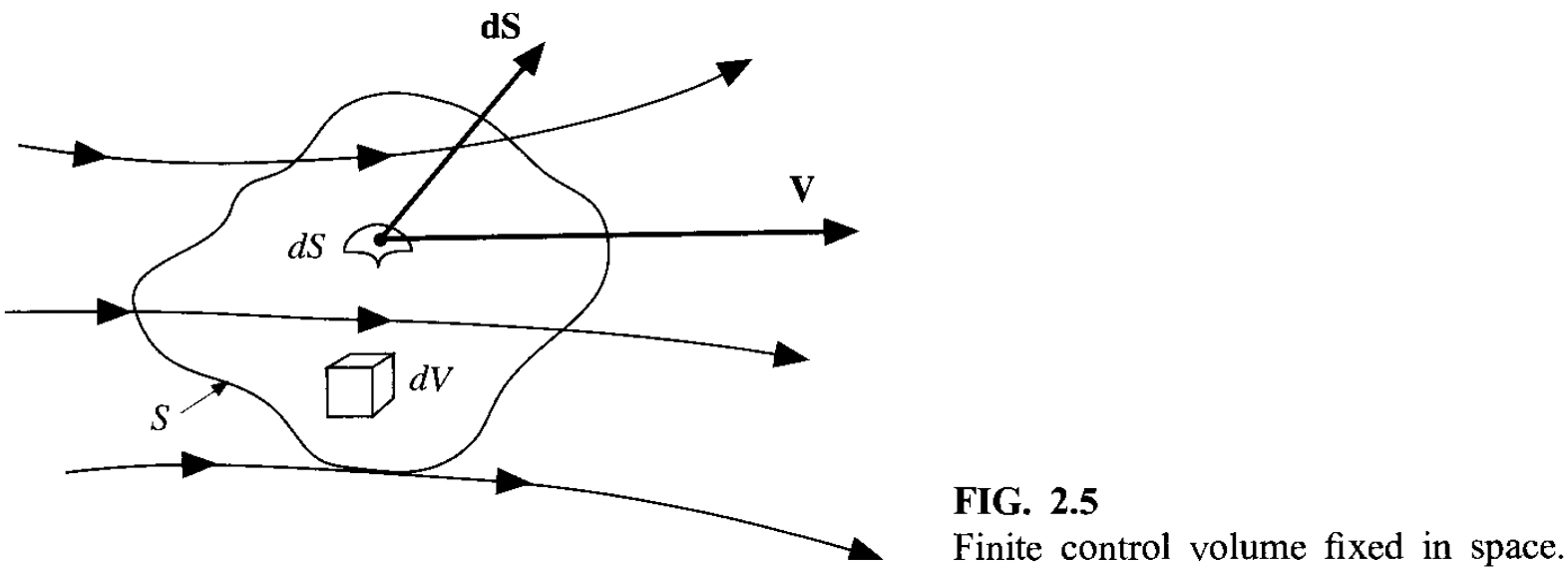
对于 BB 来说，控制体表面的某个表面单元，分析如下

  • 通过该表面单元流出的质量流量
  • 也就是，密度 × 表面积 ×流出速度垂直于表面的分量
  • 也就是， ρUndS=ρU⋅dS⃗\rho U_n dS = \rho U \cdot d\vec S

无论从数学积分角度还是物理角度，我们都认定 dS⃗d\vec S 的正方向是从控制体指向外。

  • 如果速度也向外，ρU⋅dS⃗\rho U \cdot d\vec S 就是正的，从物理上说就是流体离开控制体
  • 如果速度向内，ρU⋅dS⃗\rho U \cdot d\vec S 就是负的，物理上也就是流体进入控制体

对整个控制体表面积分，有

B=∬SρU⋅dS⃗B = \iint_S \rho U \cdot d\vec S

对于 CC 来说，

  • 控制体总质量为 ∭VρdV\iiint_V \rho dV
  • 总质量的时间变化为总质量对时间的求导
  • 控制体求导是偏导不是全导（没有对流影响）
  • 数学上，直接求导得到是的增长，而不是减少

所以

C=−∂∂t∭VρdVC = -\frac{\partial }{\partial t} \iiint_V \rho dV

根据守恒关系 B=CB = C

∂∂t∭VρdV+∬SρU⋅dS⃗=0\frac{\partial }{\partial t} \iiint_V \rho dV + \iint_S \rho U \cdot d\vec S = 0

  • 控制体的体积分和时间无关
  • 散度定理处理面积分项

上式处理为

∫V[∂∂tρ+∇⋅(ρU)]dV=0(2)\int_V[\frac{\partial}{\partial t}\rho + \nabla\cdot(\rho U)]dV = 0 \tag{2}

方程（2）为质量方程的守恒型积分形式

  • 守恒型是因为方程来自于物理量的守恒关系
  • 积分是因为体积的积分计算
  • 欧拉法

物质体微元模型

取一个无穷小物质体，

|450

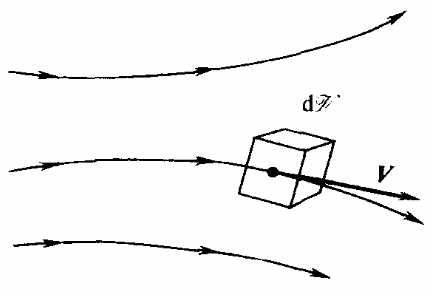
对于这个物质体微元，它的质量有

δm=ρδV\delta m = \rho \delta V

物质体微元的质量是不随时间变化的

D(δm)Dt=0\frac{D(\delta m)}{Dt} = 0

根据微积分原理可以拆写（注意这里体积也是随时间变化的）

D(ρδV)Dt=δVDρDt+ρD(δV)Dt=0\frac{D(\rho \delta V)}{Dt} = \delta V \frac{D\rho}{Dt} + \rho \frac{D(\delta V)}{Dt} = 0

整理为

DρDt+ρ[1δVD(δV)Dt]=0\frac{D\rho}{Dt} + \rho[\frac{1}{\delta V}\frac{D(\delta V)}{Dt}] = 0

再根据前文速度散度的讨论，最终为

DρDt+ρ∇⋅U=0(3)\frac{D\rho}{Dt} + \rho \nabla \cdot U = 0 \tag{3}

方程（3）为质量方程的非守恒型微分形式

  • 非守恒是因为没有用到守恒关系
  • 微分形式是因为模型的无穷小
  • 拉格朗日法

控制体微元模型

我们考虑一个无穷小控制体，

|450

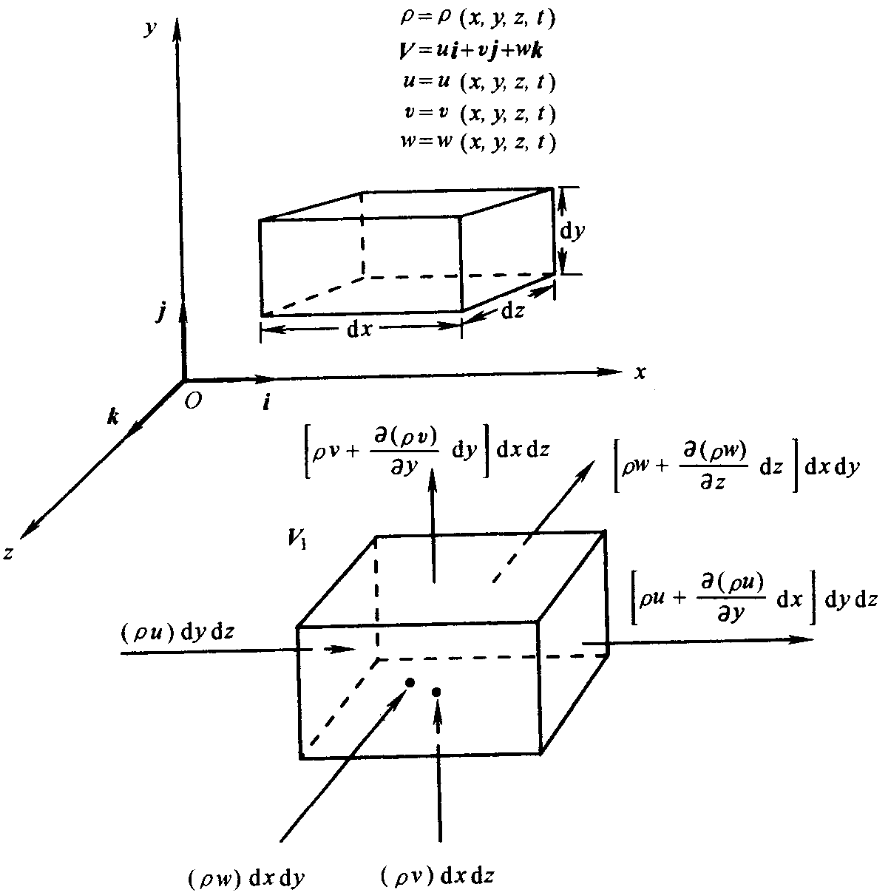
在这个无穷小控制体上，速度等物理量作为连续函数，可以进行泰勒展开。

以 x 方向为例，左面质量流量为

(ρu)dydz(\rho u)dydz

根据连续物理量的泰勒展开，右边有

ρu+∂ρu∂xdx+∂2(ρu)2!∂x2dx2+(higherOrder)\rho u + \frac{\partial \rho u}{\partial x}dx + \frac{\partial ^2 (\rho u)}{2! \partial x^2}{dx^2} + (higherOrder)

基于控制体微元的无穷小假定，省去二阶及以上的高阶项，为

[ρu+∂(ρu)∂xdx]dydz[\rho u + \frac{\partial (\rho u)}{\partial x}dx]dydz

两面之间的流量差就可以计算出来

[ρu+∂(ρu)∂xdx]dydz−(ρu)dydz=∂(ρu)∂xdxdydz[\rho u + \frac{\partial (\rho u)}{\partial x}dx]dydz - (\rho u)dydz = \frac{\partial (\rho u)}{\partial x}dxdydz

同理，y 和 z 方向的净流出量为

[ρv+∂(ρv)∂ydy]dxdz−(ρv)dxdz=∂(ρv)∂ydxdydz[\rho v + \frac{\partial (\rho v)}{\partial y}dy]dxdz - (\rho v)dxdz = \frac{\partial (\rho v)}{\partial y}dxdydz

[ρw+∂(ρw)∂zdz]dxdy−(ρw)dxdy=∂(ρw)∂zdxdydz[\rho w + \frac{\partial (\rho w)}{\partial z}dz]dxdy - (\rho w)dxdy = \frac{\partial (\rho w)}{\partial z}dxdydz

控制体微元的总净质量流量为

[∂(ρu)∂x+∂(ρv)∂y+∂(ρw)∂z]dxdydz[\frac{\partial (\rho u)}{\partial x} + \frac{\partial (\rho v)}{\partial y} + \frac{\partial (\rho w)}{\partial z}]dxdydz

控制体微元内质量增加的时间变化率

∂ρ∂t(dxdydz)\frac{\partial \rho}{\partial t}(dxdydz)

控制体微元的净质量流量必须等于其质量的减少，所以

[∂(ρu)∂x+∂(ρv)∂y+∂(ρw)∂z]dxdydz=−∂ρ∂t(dxdydz)[\frac{\partial (\rho u)}{\partial x} + \frac{\partial (\rho v)}{\partial y} + \frac{\partial (\rho w)}{\partial z}]dxdydz = -\frac{\partial \rho}{\partial t}(dxdydz)

∂ρ∂t+[∂(ρu)∂x+∂(ρv)∂y+∂(ρw)∂z]=0\frac{\partial \rho}{\partial t} + [\frac{\partial (\rho u)}{\partial x} + \frac{\partial (\rho v)}{\partial y} + \frac{\partial (\rho w)}{\partial z}] = 0

最终得到

∂ρ∂t+∇⋅(ρU)=0(4)\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho U) = 0 \tag{4}

方程（4）为质量方程的守恒型微分形式。

  • 守恒型是因为用到了守恒关系
  • 微分形式是因为模型的无穷小
  • 欧拉法

关于上式中 ρU\rho U 的散度，

回忆一下，方程（4）的左边第一项表达的是单位时间单位体积的质量变化，等于单位时间单位体积的质量流量，也就是单位体积的质量通量（质量通量等于单位时间的质量流量），也就是等于方程（4）的左边第二项。

这就说明 ∇⋅(ρU)\nabla \cdot (\rho U) 的物理意义是单位体积的质量通量（单位时间单位体积的质量流量）。

回忆前文关于速度散度的讨论。我们按照类似的思路再次理解速度散度，∇⋅U\nabla \cdot U 缺少密度，物理意义应该是单位体积的体积通量，其实就是单位时间单位体积的体积变化，和之前的讨论是一样的。

各个形式的换算

其实我们可以直接由雷诺输运定义写出方程

雷诺输运定理如下：

(dBdt)MV=∫V[DDt(ρb)+ρb∇⋅U]dV=∫V[∂∂t(ρb)+∇⋅(ρUb)]dV(\frac{dB}{dt})_{MV} = \int_V[\frac{D}{D t}(\rho b) + \rho b \nabla \cdot U]dV = \int_V[\frac{\partial}{\partial t}(\rho b) + \nabla \cdot (\rho U b)]dV

质量方程只考虑质量的输运，所以

  • B=mB = m
  • b=1b = 1

所以上式改成

DDt∭VρdV=∫V[∂∂tρ+∇⋅(ρU)]dV=∫V[DDtρ+ρ∇⋅U]dV=0\frac{D}{Dt}\iiint_V \rho dV = \int_V[\frac{\partial}{\partial t}\rho + \nabla \cdot (\rho U)]dV = \int_V[\frac{D}{D t}\rho + \rho \nabla \cdot U]dV = 0

该式是方程（1），方程（2）的综合形式。

因为物质体和控制体是任意选取的，所以上式的被积部分也处处为零，被积部分就是方恒（3）和方程（4）。

注意，利用物质导数进行下面的展开是错误的

DDt∭VρdV=∭V[∂ρ∂t+U⋅∇ρ]dV=0\cancel{\frac{D}{Dt}\iiint_V \rho dV = \iiint_V [\frac{\partial \rho}{\partial t} + U \cdot \nabla \rho]dV= 0}

因为这里的研究模型是物质体，物质体的体积是可能随着时间变化的。只有当我们假设体积也不随时间变化的时候，也就是 ∇⋅U=0\nabla \cdot U = 0 （见速度散度的讨论）的情况下。

此时直接展开有

DDt∭VρdV=∭V[∂ρ∂t+U⋅∇ρ]dV=∭V[∂ρ∂t+∇⋅(ρU)−ρ∇⋅U]dV=∫V[∂ρ∂t+∇⋅(ρU)]dV\begin{aligned} \frac{D}{Dt}\iiint_V \rho dV &= \iiint_V [\frac{\partial \rho}{\partial t} + U \cdot \nabla \rho]dV \\ &= \iiint_V [\frac{\partial \rho}{\partial t} + \nabla\cdot(\rho U) - \rho\nabla\cdot U]dV \\ &= \int_V[\frac{\partial \rho}{\partial t} + \nabla\cdot(\rho U)]dV \end{aligned}

这个结果和雷诺输运定理是一致的。

从数学上来看，积分形式的被积函数可以出现间断，微分形式的方程则要求必须是可微的，也就必须是连续的。散度定理要求数学上的连续性。当流动包含间断的时候，如激波，形式的选择就非常重要。

总的来说，基于物质导数和散度展开，始终有非守恒型和守恒型之间的换算关系

这里姑且称为【雷诺输运换算】

DDt(ρb)+ρb∇⋅U=∂∂t(ρb)+∇⋅(ρUb)\frac{D}{D t}(\rho b) + \rho b \nabla \cdot U = \frac{\partial}{\partial t}(\rho b) + \nabla \cdot (\rho U b)

这个换算关系进一步的

右边第一项展开

∂(ρb)∂t=ρ∂b∂t+b∂ρ∂t\frac{\partial (\rho b)}{\partial t} = \rho\frac{\partial b}{\partial t} + b \frac{\partial\rho}{\partial t}

移项得

ρ∂b∂t=∂(ρb)∂t−b∂ρ∂t\rho\frac{\partial b}{\partial t}=\frac{\partial (\rho b)}{\partial t} - b \frac{\partial\rho}{\partial t}

右边第二项展开（这里不明白的要去补散度计算）

∇⋅(ρUb)=b∇⋅(ρU)+(ρU)⋅∇b\nabla \cdot (\rho U b) = b \nabla \cdot (\rho U) + (\rho U) \cdot \nabla b

整理一下

ρU⋅∇b=∇⋅(ρUb)−b∇⋅(ρU)\rho U \cdot \nabla b = \nabla \cdot (\rho Ub) - b \nabla \cdot (\rho U)

代入物质导数

ρDbDt=ρ∂b∂t+ρU⋅∇b\rho\frac{Db}{Dt} = \rho\frac{\partial b}{\partial t} + \rho U\cdot \nabla b

有

ρDbDt=[∂(ρb)∂t−b∂ρ∂t]+[∇⋅(ρUb)−b∇⋅(ρU)]\rho\frac{Db}{Dt} =[ \frac{\partial (\rho b)}{\partial t} - b \frac{\partial\rho}{\partial t}] + [\nabla \cdot (\rho Ub)-b \nabla \cdot (\rho U)]

整理一下

ρDbDt=∂(ρb)∂t−b[∂ρ∂t+∇⋅(ρU)]+∇⋅(ρUb)\rho\frac{Db}{Dt} = \frac{\partial (\rho b)}{\partial t} - b[ \frac{\partial\rho}{\partial t} + \nabla \cdot (\rho U)] + \nabla \cdot (\rho Ub)

右侧中间项为质量方程的守恒微分形式，等于零

所以，有【物质导数换算】

ρDbDt=ρ∂b∂t+ρU⋅∇b=∂(ρb)∂t+∇⋅(ρUb)\rho\frac{Db}{Dt} = \rho\frac{\partial b}{\partial t} + \rho U\cdot \nabla b = \frac{\partial (\rho b)}{\partial t} + \nabla \cdot (\rho Ub)

结合【雷诺输运换算】

DDt(ρb)+ρb∇⋅U=∂∂t(ρb)+∇⋅(ρUb)\frac{D}{D t}(\rho b) + \rho b \nabla \cdot U = \frac{\partial}{\partial t}(\rho b) + \nabla \cdot (\rho U b)

代入后整理有

ρDbDt=DDt(ρb)+ρb∇⋅U\rho\frac{Db}{Dt} = \frac{D}{D t}(\rho b) + \rho b \nabla \cdot U

如果流动是不可压的（∇⋅U=0\nabla\cdot U = 0），则有

ρDbDt=DDt(ρb)\rho\frac{Db}{Dt} = \frac{D}{D t}(\rho b)

该方程的积分形式也被称为雷诺第二输运方程。

关于质量方程的积分形式和微分形式、守恒形式和非守恒形式，相信读者已经完全了解其中的关系和换算。

各种形式的换算看起来有点乱糟糟的。为了让读者摆脱这种乱糟糟的感觉却又正是换算讨论的目的。请读者亲自手算各种表达式。

补充讨论

  1. 上面的方程推导过程中，没有作多余的假设，所以适用于任何类型的流体。

  2. 质量方程的守恒型微分形式

∂ρ∂t+∇⋅(ρU)=0\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho U) = 0

展开就是

∂ρ∂t+∂ρu∂x+∂ρv∂y+∂ρw∂z=0 \frac{\partial \rho}{\partial t} + \frac{\partial \rho u}{\partial x}+\frac{\partial \rho v}{\partial y} +\frac{\partial \rho w}{\partial z} = 0

  1. OpenFOAM 中使用有限体积法，所以质量方程使用守恒型积分形式

∫V[∂∂tρdV+∇⋅(ρU)]dV=0\int_V[\frac{\partial}{\partial t}\rho dV + \nabla\cdot(\rho U)]dV = 0

  1. 对于不可压缩流动，密度是恒定的（不随时间和空间变化）

注意此处“密度恒定”不是说密度在流动中处处恒定，而是说密度在特定的流线上恒定（如果困惑的话，回忆前文的讨论，即对时间的全微分计算某种程度上来说是拉格朗日法的）

DρDt=0\frac{D\rho}{Dt} = 0

根据 质量方程的非守恒微分形式，

DρDt+ρ∇⋅U=0\frac{D\rho}{Dt} + \rho \nabla \cdot U = 0

可以进一步得到

∇⋅U=0\nabla \cdot U = 0

速度的散度是单位时间单位体积的体积变化，不可压缩流体的速度散度为零，也正说明了它的体积不会变化，也就是不可压缩。

  1. 对于定常流动，密度不随时间变化（不同位置的密度有可能不同，所以仅对时间偏导为零）

∂ρ∂t=0\frac{\partial \rho}{\partial t} = 0

根据质量方程的守恒微分形式

∂ρ∂t+∇⋅(ρU)=0\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho U) = 0

可以得到

∇⋅(ρU)=0\nabla \cdot (\rho U) = 0

也就是研究模型的质量通量为零（这个模型和外界没有质量交换，也就是定常流体）。

相信读者手推公式后，能领会到其中来来回回都能圆满自洽的快乐。

动量方程

F⃗=ma⃗\vec F = m \vec a

分量表达

我们采用无穷小物质体模型来讨论动量方程，相信会更加容易理解。

|425

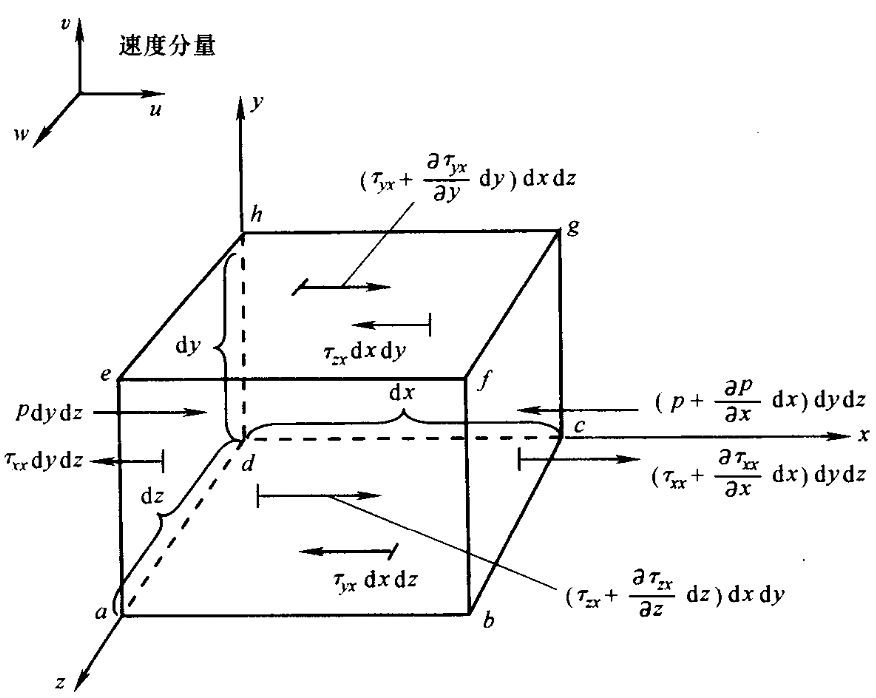
这个模型将得到动量方程的守恒型微分形式。

考虑 x 方向，有

Fx=maxF_x = m a_x

受力分析

受到力的构成分成 2 部分，

  • 体积力，直接作用在整个物质体的体积微元上，与质量有紧密关系，超距离，比如重力、电场力、磁场力等
    • 数学表达为 ρf(dxdydz)\rho f(dxdydz)
  • 表面力，直接作用在模型的表面，有 2 个来源
    • 物质体微元周围的流体作用于微元表面的压力分布，压力是一种正压力，始终垂直于作用面
    • 外部流体推拉摩擦微元表面的剪切力（包括切应力和正应力）分布

|400

正应力和切应力都依赖于流体的速度梯度，和形变的速率成正比。应力越大，形变的速度越快。大多数粘性流动中，正应力都比切应力小的多，乃至可以忽略不计，当法向速度梯度很大时 (例如激波内部)，正应力就变得重要

我们约定用 τij\tau_{ij} 表示 沿着j 方向的应力作用在垂直于 i 轴的平面上。我们分析出图中 x 方向的所有力。

x 方向的表面力 FxF_x 为

Fx=(p−(p+∂p∂xdx))dydz+((τxx+∂τxx∂xdx)−τxx)dydz+((τyx+∂τyx∂y)−τyx)dxdz+((τzx+∂τzx∂z)−τzx)dxdy\begin{aligned} F_x &= \bigg(p-(p+\frac{\partial p}{\partial x}dx)\bigg)dydz + \bigg((\tau_{xx}+\frac{\partial \tau_{xx}}{\partial x}dx)-\tau_{xx}\bigg)dydz \\ &+ \bigg((\tau_{yx} + \frac{\partial \tau_{yx}}{\partial y})-\tau_{yx}\bigg)dxdz + \bigg((\tau_{zx} + \frac{\partial \tau_{zx}}{\partial z})-\tau_{zx}\bigg)dxdy \end{aligned}

化简后，并考虑上体积力，有

Fx=(−∂p∂x+∂τxx∂x+∂τyx∂y+∂τzx∂z)dxdydz+ρfxdxdydz F_x = (-\frac{\partial p}{\partial x} + \frac{\partial\tau_{xx}}{\partial x} + \frac{\partial\tau_{yx}}{\partial y} + \frac{\partial\tau_{zx}}{\partial z}) dxdydz + \rho f_x dxdydz

运动流体微元的质量为

m=ρdxdydzm = \rho dxdydz

考虑流体微元的加速度，x 方向应该有

ax=DuDta_x = \frac{Du}{Dt}

综合上式，而且两边同时除以 dxdydzdxdydz

ρDuDt=−∂p∂x+∂τxx∂x+∂τyx∂y+∂τzx∂z+ρfx\rho\frac{Du}{Dt} = -\frac{\partial p}{\partial x} + \frac{\partial\tau_{xx}}{\partial x} + \frac{\partial\tau_{yx}}{\partial y} + \frac{\partial\tau_{zx}}{\partial z} + \rho f_x

同样的，y 方向和 z 方向也有

ρDvDt=−∂p∂y+∂τxy∂x+∂τyy∂y+∂τzy∂z+ρfy\rho\frac{Dv}{Dt} = -\frac{\partial p}{\partial y} + \frac{\partial\tau_{xy}}{\partial x} + \frac{\partial\tau_{yy}}{\partial y} + \frac{\partial\tau_{zy}}{\partial z} + \rho f_y

ρDwDt=−∂p∂z+∂τxz∂x+∂τyz∂y+∂τzz∂z+ρfz\rho\frac{Dw}{Dt} = -\frac{\partial p}{\partial z} + \frac{\partial\tau_{xz}}{\partial x} + \frac{\partial\tau_{yz}}{\partial y} + \frac{\partial\tau_{zz}}{\partial z} + \rho f_z

分量形式

根据物质导数换算关系

ρDuDt=ρ∂u∂t+ρU⋅∇u=∂(ρu)∂t+∇⋅(ρuU) \rho\frac{Du}{Dt} = \rho\frac{\partial u}{\partial t} + \rho U \cdot \nabla u = \frac{\partial (\rho u)}{\partial t} + \nabla \cdot (\rho u U)

最终有 N-S 方程

∂(ρu)∂t+∇⋅(ρuU)=−∂p∂x+∂τxx∂x+∂τyx∂y+∂τzx∂z+ρfx\frac{\partial (\rho u)}{\partial t} + \nabla \cdot (\rho u U) = -\frac{\partial p}{\partial x} + \frac{\partial\tau_{xx}}{\partial x} + \frac{\partial\tau_{yx}}{\partial y} + \frac{\partial\tau_{zx}}{\partial z} + \rho f_x

∂(ρv)∂t+∇⋅(ρvU)=−∂p∂y+∂τxy∂x+∂τyy∂y+∂τzy∂z+ρfy\frac{\partial (\rho v)}{\partial t} + \nabla \cdot (\rho v U) = -\frac{\partial p}{\partial y} + \frac{\partial\tau_{xy}}{\partial x} + \frac{\partial\tau_{yy}}{\partial y} + \frac{\partial\tau_{zy}}{\partial z} + \rho f_y

∂(ρw)∂t+∇⋅(ρwU)=−∂p∂z+∂τxz∂x+∂τyz∂y+∂τzz∂z+ρfz\frac{\partial (\rho w)}{\partial t} + \nabla \cdot (\rho w U) = -\frac{\partial p}{\partial z} + \frac{\partial\tau_{xz}}{\partial x} + \frac{\partial\tau_{yz}}{\partial y} + \frac{\partial\tau_{zz}}{\partial z} + \rho f_z

上面的分量形式仍然有很多和流体相关的项需要讨论。

流体应力

到了 17 世纪末，牛顿指出，流体的切应力与应变的时间变化率（也就是速度梯度）成正比，这样的流体也被称为牛顿流体 。

在空气动力学的所有实际问题中，流体都可以被看成牛顿流体，斯托克斯得到有

τxx=λ(∇⋅U)+2μ∂u∂x\tau_{xx} = \lambda(\nabla\cdot U) + 2\mu\frac{\partial u}{\partial x}

τyy=λ(∇⋅U)+2μ∂v∂y\tau_{yy} = \lambda(\nabla\cdot U) + 2\mu\frac{\partial v}{\partial y}

τzz=λ(∇⋅U)+2μ∂w∂z\tau_{zz} = \lambda(\nabla\cdot U) + 2\mu\frac{\partial w}{\partial z}

τxy=τyx=μ(∂v∂x+∂u∂y)\tau_{xy} = \tau_{yx} = \mu(\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y})

τxz=τzx=μ(∂u∂z+∂w∂x)\tau_{xz} = \tau_{zx} = \mu(\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x})

τyz=τzy=μ(∂w∂y+∂v∂z)\tau_{yz} = \tau_{zy} = \mu(\frac{\partial w}{\partial y} + \frac{\partial v}{\partial z})

其中，μ\mu 是分子粘性系数，λ\lambda 是第二粘性系数，斯托克斯进一步假设有

λ=−23μ\lambda = -\frac{2}{3}\mu

将物性关系代入获得完整动量方程。

张量表达

方程的分量形式非常繁琐，不利于理论表达和分析，我们采用张量形式进行分析推导和表达。

根据牛顿定理

F⃗t=mU\vec Ft = m U

物质体上应用牛顿定理有

(d(mU)dt)MV=(∫Vf⃗dV)MV\bigg(\frac{d(mU)}{dt}\bigg)_{MV} = \bigg(\int_V \vec f dV\bigg)_{MV}

其中 f⃗\vec{f} 是单位体积的外力，包含表面力和体积力。

方程左侧根据雷诺输运定理，可以分别写成守恒型和非守恒型的方程。

非守恒型

∫V[DDt(ρU)+ρU∇⋅U]dV−∫Vf⃗dV=0\int_V[\frac{D}{D t}(\rho U) + \rho U \nabla \cdot U]dV - \int_V \vec f dV = 0

整理可得

∫V[DDt(ρU)+ρU∇⋅U−f⃗]dV=0\int_V[\frac{D}{D t}(\rho U) + \rho U \nabla \cdot U - \vec f]dV = 0

脱去积分

DDt(ρU)+ρU∇⋅U=f⃗\frac{D}{D t}(\rho U) + \rho U \nabla \cdot U = \vec f

展开上式可得

(ρDUDt+UDρDt)+ρU∇⋅U=f⃗(\rho\frac{DU}{Dt} + U\frac{D\rho}{Dt}) + \rho U \nabla \cdot U = \vec f

整理

ρDUDt+U(DρDt+ρ∇⋅U)=f⃗\rho\frac{DU}{Dt} + U(\frac{D\rho}{Dt} + \rho \nabla \cdot U) = \vec f

注意左侧第二项括号内是质量方程的非守恒型微分形式，等于零，

所以有

ρDUDt=f⃗\rho\frac{DU}{Dt}= \vec f

根据物质导数，有

ρ∂U∂t+ρU⋅∇U=f⃗\rho\frac{\partial U}{\partial t} + \rho U\cdot \nabla U= \vec f

守恒型

根据雷诺输运定理将牛顿定理的应用写成守恒型

∫V[∂∂t(ρU)+∇⋅(ρUU)]dV−∫Vf⃗dV=0\int_V[\frac{\partial}{\partial t}(\rho U) + \nabla \cdot (\rho U U)]dV - \int_V \vec f dV = 0

合并积分，整理后有

∂∂t(ρU)+∇⋅(ρUU)=f⃗\frac{\partial}{\partial t}(\rho U) + \nabla \cdot (\rho UU) = \vec f

注意该式就是前文分量形式的矢量写法。

外力的构成

外力可以分成表面力和体积力

f⃗=f⃗s+f⃗b\vec f = \vec f_s + \vec f_b

表面力

在表面的一个面积微元上，表面力等于总应力张量和面矢量的积（力 = 应力×面积）

df⃗s=Σ⋅dS⃗=Σ⋅n⃗dSd\vec f_s = \Sigma \cdot d\vec S = \Sigma\cdot \vec n dS

使用 Σ\Sigma 表示总应力张量（stress tensor)（完整包含正应力和切应力）

Σ=[ΣxxΣxyΣxzΣyxΣxxΣyzΣzxΣzyΣzz]\Sigma = \begin{bmatrix} \Sigma_{xx} & \Sigma_{xy} & \Sigma_{xz} \\ \Sigma_{yx} & \Sigma_{xx} & \Sigma_{yz} \\ \Sigma_{zx} & \Sigma_{zy} & \Sigma_{zz} \end{bmatrix}

  • 相同下标 Σii\Sigma_{ii} 表示法向应力，大于零为受拉（tension），小于零为受压（compression）。导致法向应力的主要物理原因是压力，很小一部分原因才是粘性
  • 不同下标 Σij\Sigma_{ij} 表示切向应力，表示 ii 面上 jj 方向（ii 面为垂直 ii 方向的面，与分量形式的约定一样），约定如果面的外法向为正，则 ii 为正。导致切向应力的物理原因是粘性

注意压力只在法向上，而且压力没有受拉，只有受压，也就是只有负值，所以应力张量其实可以写成

Σ=−[p000p000p]+{τxxτxyτxzτyxτyyτyzτzxτzyτzz} \Sigma = - \begin{bmatrix} p & 0 & 0 \\ 0 & p & 0 \\ 0 & 0 & p \end{bmatrix} + \begin{Bmatrix} \tau_{xx} & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & \tau_{yy} & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & \tau_{zz} \end{Bmatrix}

我们简化表示为

Σ={τxx−pτxyτxzτyxτyy−pτyzτzxτzyτzz−p}=−pI⃗+τ⃗\Sigma =\begin{Bmatrix} \tau_{xx} - p & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & \tau_{yy}-p & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & \tau_{zz} - p \end{Bmatrix} = -p\vec I + \vec{\tau}

也就是说，总应力张量可以分解为压力和粘性力。

整个表面的表面力等于面单元的表面力的面积分

∫Vf⃗sdV=∫SΣ⋅n⃗dS\int_V\vec f_sdV = \int_S \Sigma\cdot \vec n dS

再利用散度定理如下

∫SΣ⋅n⃗dS=∫V∇⋅ΣdV\int_S \Sigma\cdot \vec n dS = \int_V\nabla\cdot\Sigma dV

代入上式有

f⃗S=[∇⋅Σ]=−∇p+[∇⋅τ]\vec f_S = [\nabla\cdot\Sigma] = -\nabla p + [\nabla\cdot \tau]

粘性力

在上面的推导中，表面力中的粘性力部分仍然未知，对于牛顿流体来说，有本构关系

τ⃗=μ[∇U+(∇U)T]+λ(∇⋅U)I⃗\vec{\tau} = \mu [\nabla U + (\nabla U)^T] + \lambda(\nabla\cdot U)\vec I

（请参考前文讨论的流体应力分量表达式）

  • 如果流体是可压的

斯托克斯假设

λ=−23μ\lambda = - \frac{2}{3} \mu

此时粘性力完整表达为

τ⃗=μ[∇U+(∇U)T]−23μ(∇⋅U)I⃗ \vec{\tau} = \mu [\nabla U + (\nabla U)^{T}] - \frac{2}{3}\mu (\nabla\cdot U)\vec I

  • 如果流体是不可压的

根据前文讨论，有

∇⋅U=0\nabla\cdot U = 0

此时，粘性力简化为

τ⃗=μ[∇U+(∇U)T]\vec{\tau} = \mu [\nabla U + (\nabla U)^T]

结合这些讨论，也就可以理解为什么 λ(∇⋅U)\lambda(\nabla\cdot U) 这一项也被为体积膨胀率。

引入应变率（strain rate），也被称为形变率，可以表示成速度的函数

S=[SxxSxySxzSyxSyySyzSzxSzySzz]=[12(∂u∂x+∂u∂x)12(∂u∂y+∂v∂x)12(∂u∂z+∂w∂x)12(∂v∂x+∂u∂y)12(∂v∂y+∂v∂y)12(∂v∂z+∂w∂y)12(∂w∂x+∂u∂z)12(∂w∂y+∂v∂z)12(∂w∂z+∂w∂z)] \begin{align*} S &= \begin{bmatrix} S_{xx} &S_{xy} &S_{xz}\\ S_{yx} &S_{yy} &S_{yz}\\ S_{zx} &S_{zy} &S_{zz} \end{bmatrix}\\ &= \begin{bmatrix} \frac{1}{2}\left(\frac{\partial u}{\partial x} + \frac{\partial u}{\partial x}\right)& \frac{1}{2}\left(\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\right)& \frac{1}{2}\left(\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x}\right)\\ \frac{1}{2}\left(\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}\right)& \frac{1}{2}\left(\frac{\partial v}{\partial y} + \frac{\partial v}{\partial y}\right)& \frac{1}{2}\left(\frac{\partial v}{\partial z} + \frac{\partial w}{\partial y}\right)\\ \frac{1}{2}\left(\frac{\partial w}{\partial x} + \frac{\partial u}{\partial z}\right)& \frac{1}{2}\left(\frac{\partial w}{\partial y} + \frac{\partial v}{\partial z}\right)& \frac{1}{2}\left(\frac{\partial w}{\partial z} + \frac{\partial w}{\partial z}\right)\\ \end{bmatrix} \end{align*}

写成矢量形式

S=12(∇U+∇UT) S = \frac{1}{2} (\nabla U + \nabla U^{T})

粘性力表达为

τ⃗=2μS \vec{\tau} = 2\mu S

注意 μ\mu 仍然是流体粘度，是流体的物理属性。

体积力

主要是重力，给出如下

f⃗b=ρg⃗\vec f_b = \rho \vec g

对于旋转系统来说，体力还来自于科里奥利力 和向心力

f⃗b=−2ρ[ω×U]−ρ[ω×[ω×r⃗]]\vec f_b = -2\rho[\omega \times U] - \rho [\omega\times[\omega\times\vec r]]

一般来说，重力和向心力都和位置有关，和速度无关，所以会归在压力修正项中。科里奥利力会单独处理。体积力像是还有电磁力电场力等多种类型需要针对具体问题进行处理，所以下面方程中的体积力不再写成具体形式。

张量形式

考虑最一般情况，动量方程守恒型微分形式为

∂∂t(ρU)+∇⋅(ρUU)=−∇p+(∇⋅τ⃗)+f⃗b\frac{\partial}{\partial t}(\rho U) + \nabla \cdot (\rho UU) = -\nabla p + (\nabla\cdot\vec{\tau}) + \vec f_b

使用 OpenFOAM 表示符号

∂∂t(ρU)+∇⋅(ρUU)=−∇p+(∇⋅rhoReff)+f⃗b\frac{\partial}{\partial t}(\rho U) + \nabla \cdot (\rho UU) = -\nabla p + (\nabla\cdot rhoR^{eff}) + \vec f_b

流体粘性应力的张量形式

rhoReff=μ[∇U+(∇U)T]+λ(∇⋅U)I⃗rhoR^{eff} = \mu [\nabla U + (\nabla U)^{T}] + \lambda(\nabla\cdot U)\vec I

展开成矩阵形式更加清楚

rhoReff=[2μ∂u∂x+λ∇⋅Uμ(∂v∂x+∂u∂y)μ(∂u∂z+∂w∂x)μ(∂v∂x+∂u∂y)2μ∂v∂y+λ(∇⋅U)μ(∂w∂y+∂v∂z)μ(∂u∂z+∂w∂x)μ(∂w∂y+∂v∂z)2μ∂w∂z+λ(∇⋅U)]rhoR^{eff} = \begin{bmatrix} 2\mu\frac{\partial u}{\partial x} + \lambda\nabla\cdot U & \mu(\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}) & \mu(\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x}) \\ \mu(\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}) & 2\mu\frac{\partial v}{\partial y} + \lambda(\nabla\cdot U) & \mu(\frac{\partial w}{\partial y} + \frac{\partial v}{\partial z}) \\ \mu(\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x}) & \mu(\frac{\partial w}{\partial y} + \frac{\partial v}{\partial z}) & 2\mu\frac{\partial w}{\partial z} + \lambda(\nabla\cdot U) \end{bmatrix}

粘性应力张量的散度为

∇⋅τ⃗=∇⋅[μ(∇U+(∇U)T)]+∇(λ∇⋅U)={∂∂x[2μ∂u∂x+λ∇⋅U]+∂∂y[μ(∂v∂x+∂u∂y)]+∂∂z[μ(∂u∂z+∂w∂x)]∂∂x[μ(∂v∂x+∂u∂y)]+∂∂y[2μ∂v∂y+λ(∇⋅U)]+∂∂z[μ(∂w∂y+∂v∂z)]∂∂x[μ(∂u∂z+∂w∂x)]+∂∂y[μ(∂w∂y+∂v∂z)]+∂∂z[2μ∂w∂z+λ(∇⋅U)]}\begin{aligned} \nabla\cdot \vec{\tau} &= \nabla\cdot[\mu (\nabla U + (\nabla U)^T)] + \nabla(\lambda\nabla\cdot U) \\ &= \begin{Bmatrix} \frac{\partial}{\partial x}[2\mu\frac{\partial u}{\partial x} + \lambda\nabla\cdot U] + \frac{\partial}{\partial y}[\mu(\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y})] +\frac{\partial}{\partial z}[\mu(\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x})] \\ \frac{\partial}{\partial x}[\mu(\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y})] + \frac{\partial}{\partial y}[2\mu\frac{\partial v}{\partial y} + \lambda(\nabla\cdot U)] + \frac{\partial}{\partial z}[\mu(\frac{\partial w}{\partial y} + \frac{\partial v}{\partial z})] \\ \frac{\partial}{\partial x}[\mu(\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x})] + \frac{\partial}{\partial y}[\mu(\frac{\partial w}{\partial y} + \frac{\partial v}{\partial z})] +\frac{\partial}{\partial z}[2\mu\frac{\partial w}{\partial z} + \lambda(\nabla\cdot U)] \end{Bmatrix} \end{aligned}

代入动量方程守恒型微分形式，得到

∂∂t(ρU)+∇⋅(ρUU)=−∇p+∇⋅[μ(∇U+(∇U)T)]+∇(λ∇⋅U)+f⃗b\frac{\partial}{\partial t}(\rho U) + \nabla \cdot (\rho UU) = -\nabla p + \nabla\cdot[\mu (\nabla U + (\nabla U)^T)] + \nabla(\lambda\nabla\cdot U) + \vec f_b

其中

∇⋅[μ(∇U+(∇U)T)]=∇⋅(μ∇U)+∇⋅[μ(∇U)T]\nabla\cdot[\mu (\nabla U + (\nabla U)^{T})] = \nabla\cdot(\mu\nabla U) + \nabla\cdot[\mu (\nabla U)^{T}]

整理为

∂∂t(ρU)+∇⋅(ρUU)=∇⋅(μ∇U)−∇p+∇⋅[μ(∇U)T]+∇(λ∇⋅U)+f⃗b\frac{\partial}{\partial t}(\rho U) + \nabla \cdot (\rho UU) = \nabla\cdot(\mu\nabla U)-\nabla p + \nabla\cdot[\mu (\nabla U)^T] + \nabla(\lambda\nabla\cdot U) + \vec f_b

对于更一般的情况，将右边后三项统一为广义源项，整理为

∂∂t(ρU)+∇⋅(ρUU)−∇⋅(μ∇U)=−∇p+Q \frac{\partial}{\partial t}(\rho U) + \nabla \cdot (\rho UU) - \nabla\cdot(\mu\nabla U) = -\nabla p + Q

补充讨论

  1. 对于无粘性流动，粘性系数 μ=0\mu=0 ，动量方程最终简化为

∂∂t(ρU)+∇⋅(ρUU)=−∇p+f⃗b\frac{\partial}{\partial t}(\rho U) + \nabla \cdot (\rho UU) = -\nabla p + \vec f_b

即没有粘性扩散。

  1. 对于不可压缩流体

∇⋅U=0\nabla\cdot U = 0

动量方程简化为

∂∂t(ρU)+∇⋅(ρUU)=−∇p+∇⋅[μ(∇U+(∇U)T)]+∇(λ∇⋅U)+f⃗b\frac{\partial}{\partial t}(\rho U) + \nabla \cdot (\rho UU) = -\nabla p + \nabla\cdot[\mu (\nabla U + (\nabla U)^T)] + \cancel{\nabla(\lambda\nabla\cdot U)} + \vec f_b

对于牛顿流体，有剪切应力 τ⃗\vec{\tau} 线性相关于形变率 SS （矢量）为线性，即

τ⃗=2μS=μ(∇U+(∇U)T) \vec{\tau} = 2\mu S = \mu(\nabla U + (\nabla U)^{T})

结合 Boussnesq 假设，密度变化仅仅对浮力起作用，其他项中的密度变化可以忽略，甚至如果这里就是不可压缩流体，则有

∂∂t(ρU)+∇⋅(ρUU)=−∇p+∇⋅[μ(∇U+(∇U)T)]+∇(λ∇⋅U)+f⃗b∂U∂t+∇⋅(UU)−∇⋅[ν(∇U+(∇U)T]=−1ρ∇p+Q∂U∂t+∇⋅(UU)−∇⋅(2νS)=−1ρ∇p+Q∂U∂t+∇⋅(UU)+∇⋅Reff=−1ρ∇p+Q\begin{align*} \frac{\partial}{\partial t}(\rho U) + \nabla \cdot (\rho UU) &= -\nabla p + \nabla\cdot[\mu (\nabla U + (\nabla U)^T)] + \cancel{\nabla(\lambda\nabla\cdot U)} + \vec f_{b} \\ \frac{\partial U}{\partial t} + \nabla \cdot (UU) - \nabla \cdot[\nu(\nabla U + (\nabla U)^{T}] &= - \frac{1}{\rho} \nabla p + Q \\ \frac{\partial U}{\partial t} + \nabla \cdot (UU) - \nabla \cdot (2\nu S) &= - \frac{1}{\rho} \nabla p + Q \\ \frac{\partial U}{\partial t} + \nabla \cdot (UU) + \nabla \cdot R^{eff} &= - \frac{1}{\rho} \nabla p + Q \end{align*}

如果此时粘性系数 μ\mu 为常数，动量方程可以进一步简化

以 应力张量散度 的第一行为例，此时

(∇⋅τ)col1=∂∂x[2μ∂u∂x+λ∇⋅U]+∂∂y[μ(∂v∂x+∂u∂y)]+∂∂z[μ(∂u∂z+∂w∂x)](\nabla\cdot\tau)_{col1} = \frac{\partial}{\partial x}[2\mu\frac{\partial u}{\partial x} + \cancel{\lambda\nabla\cdot U}] + \frac{\partial}{\partial y}[\mu(\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y})] +\frac{\partial}{\partial z}[\mu(\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x})]

=μ∂∂x[2μ∂u∂x]+μ∂∂y[(∂v∂x+∂u∂y)]+μ∂∂z[(∂u∂z+∂w∂x)]= \mu\frac{\partial}{\partial x}[2\mu\frac{\partial u}{\partial x}] + \mu\frac{\partial}{\partial y}[(\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y})] +\mu\frac{\partial}{\partial z}[(\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x})]

=μ[∂2u∂x2+∂2u∂x2+∂2u∂y2+∂2v∂xy+∂2u∂z2+∂2w∂xz]=\mu[\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 v}{\partial xy} + \frac{\partial^2 u}{\partial z^2} + \frac{\partial^2 w}{\partial xz}]

=μ[(∂2u∂x2+∂2u∂y2+∂2u∂z2)+∂2u∂x2+∂2v∂xy+∂2w∂xz]= \mu[(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}+\frac{\partial^2 u}{\partial z^2}) + \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 v}{\partial xy} + \frac{\partial^2 w}{\partial xz}]

=μ[(∂2u∂x2+∂2u∂y2+∂2u∂z2)+∂∂x(∂u∂x+∂v∂y+∂w∂z)]= \mu[(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}+\frac{\partial^2 u}{\partial z^2}) + \frac{\partial }{\partial x}(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z})]

→μ[(∇2U)+∂∂x(∇⋅U)]\rightarrow \mu[(\nabla^2 U) + \frac{\partial }{\partial x}(\nabla\cdot U)]

→μ[(∇2U)+∂∂x(∇⋅U)]\rightarrow \mu[(\nabla^2 U) + \cancel{\frac{\partial }{\partial x}(\nabla\cdot U)}]

因为流体不可压缩，密度不变，第二项为零，所以动量方程进一步简化为（ pp 为密度处理后的压力）

∂U∂t+∇⋅(UU)=−∇p+ν∇2U+f⃗b\frac{\partial U}{\partial t} + \nabla \cdot (UU) = -\nabla p + \nu\nabla^2U + \vec f_b

下面参考 《OpenFOAM A Little User Manual》

在 OpenFOAM 中不可压缩流动，

Reff=−ν(∇U+(∇U)T)R^{eff} = -\nu (\nabla U + (\nabla U)^{T})

即

Ri,jeff=−ν(∂ui∂xj+∂uj∂xi)R^{eff}_{i,j} = -\nu \bigg( \frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}} \bigg)

任意应力张量可以分解成：平均应力张量（迹的平均）+ 偏应力张量

Reff=13tr(Reff)+dev(Reff)R^{eff} = \frac{1}{3}tr(R^{eff}) + dev(R^{eff})

有

tr(Reff)=Riieff−2ν(∂ui∂xi)tr(R^{eff}) = R^{eff}_{ii} -2\nu\bigg( \frac{\partial u_{i}}{\partial x_{i}} \bigg)

而

tr(Reff)=Riieff=−2νeff(∂ui∂xi)=0tr(R^{eff}) = R_{ii}^{eff}=-2\nu^{eff}\left(\frac{\partial u_{i}}{\partial x_{i}}\right)= 0

∂ui∂xi=∇⋅U=0\frac{\partial u_{i}}{\partial x_{i}} = \nabla \cdot U = 0

所以有

Reff=dev(Reff)R^{eff} = dev(R^{eff})

即

∇⋅Reff=div(devReff)\nabla\cdot R^{eff} = div(devR^{eff})

这样的简化也就在 OpenFOAM 有如下表达

∂U∂t+∇⋅(UU)−∇⋅Reff=−∇p+Q∂U∂t+∇⋅(UU)−[turbulence→divDevReff(U)]=−∇p+Q\begin{align*} \frac{\partial U}{\partial t} + \nabla \cdot (UU) - \nabla \cdot R^{eff} &= -\nabla p + Q\\ \frac{\partial U}{\partial t} + \nabla \cdot (UU) - \bigg[ turbulence \rightarrow div DevReff(U) \bigg] &= -\nabla p + Q \end{align*}

能量方程

能量守恒

分量表达

取无穷小物质体（物质体微元）为研究对象

|500

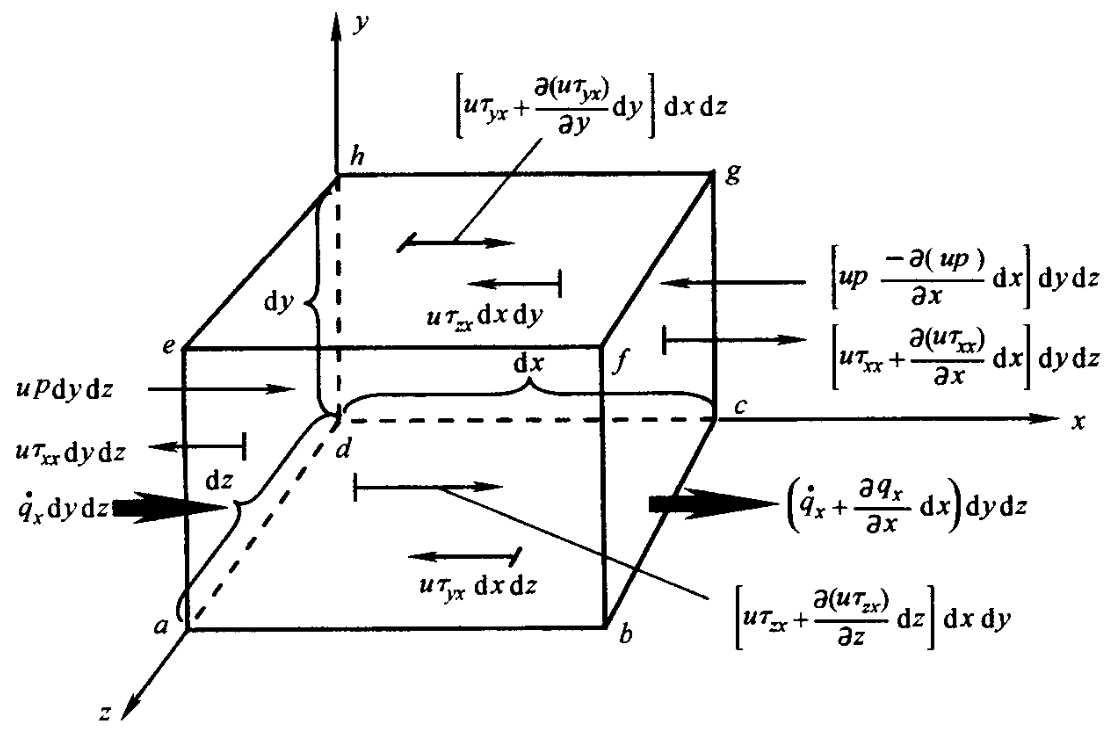
有守恒关系

物质体微元内能量的变化率 = 单位时间流入微元的净热流量 + 体积力和表面力对微元做功的功率

A=B+CA = B + C

外力做功的功率

  1. 体积力做功功率

ρf⃗⋅U(dxdydz)\rho \vec f\cdot U(dxdydz)

  1. 表面力做功功率

功率 = 力 × 面积 × 速度

以 xx 方向为例子，约定力沿着坐标轴正向做正功，相反做负功。

压力做功功率为

[up−(up+∂(up)∂x)dx]dydz=−∂(up)∂xdxdydz[up-(up+\frac{\partial(up)}{\partial x})dx]dydz = -\frac{\partial(up)}{\partial x}dxdydz

切应力做功功率为

[(uτyx+∂(uτyx)∂y)dy−uτyx]dxdz=∂(uτyx)∂ydxdydz[(u\tau_{yx}+\frac{\partial(u\tau_{yx})}{\partial y})dy-u\tau_{yx}]dxdz = \frac{\partial(u\tau_{yx})}{\partial y}dxdydz

综合 xx 方向所有表面力的做工功率为

[∂(up)∂x+∂(uτxx)∂x+∂(uτyx)∂y+∂(uτzx)∂z]dxdydz[\frac{\partial(up)}{\partial x} + \frac{\partial(u\tau_{xx})}{\partial x} + \frac{\partial(u\tau_{yx})}{\partial y} + \frac{\partial(u\tau_{zx})}{\partial z}]dxdydz

综合其他方向的表面力，最终得到 CC 为

C=[−(∂(up)∂x+∂(vp)∂y+∂(wp)∂z)+∂(uτxx)∂x+∂(uτyx)∂y+∂(uτzx)∂z+∂(vτxy)∂x+∂(vτyy)∂y+∂(vτzy)∂z+∂(wτxz)∂x+∂(wτyz)∂y+∂(wτzz)∂z]dxdydz+ρf⃗⋅U(dxdydz)\begin{aligned} C &= [-(\frac{\partial(up)}{\partial x}+\frac{\partial(vp)}{\partial y}+\frac{\partial(wp)}{\partial z}) \\ & +\frac{\partial(u\tau_{xx})}{\partial x} + \frac{\partial(u\tau_{yx})}{\partial y} + \frac{\partial(u\tau_{zx})}{\partial z} \\ &+ \frac{\partial(v\tau_{xy})}{\partial x} + \frac{\partial(v\tau_{yy})}{\partial y} + \frac{\partial(v\tau_{zy})}{\partial z} \\ &+ \frac{\partial(w\tau_{xz})}{\partial x} + \frac{\partial(w\tau_{yz})}{\partial y} + \frac{\partial(w\tau_{zz})}{\partial z}]dxdydz +\rho \vec f\cdot U(dxdydz) \end{aligned}

流入物质体微元净热流量

  1. 体积加热，如吸收释放的辐射热

ρq˙dxdydz\rho \dot qdxdydz

  1. 温度梯度导致的经过表面的热输运，即热传导
    以 xx 方向为例

[q˙x−(q˙x+∂q˙x∂xdx)]dydz=∂q˙x∂xdxdydz[\dot q_x - (\dot q_x + \frac{\partial \dot q_x}{\partial x}dx)]dydz = \frac{\partial \dot q_x}{\partial x}dxdydz

热传导的总加热为

−(∂q˙x∂x+∂q˙y∂y+∂q˙z∂z)dxdydz-(\frac{\partial \dot q_x}{\partial x}+\frac{\partial \dot q_y}{\partial y}+\frac{\partial \dot q_z}{\partial z})dxdydz

流入微元的净热流量 BB 为

B=[ρq˙−(∂q˙x∂x+∂q˙y∂y+∂q˙z∂z)]dxdydzB=[\rho \dot q-(\frac{\partial \dot q_x}{\partial x}+\frac{\partial \dot q_y}{\partial y}+\frac{\partial \dot q_z}{\partial z})]dxdydz

根据傅里叶热传导定律有

q˙i=−k∂T∂xi\dot q_i = -k\frac{\partial T}{\partial x_i}

最终

B=[ρq˙+∂∂x(k∂T∂x)+∂∂y(k∂T∂y)+∂∂z(k∂T∂z)]dxdydzB = [\rho \dot q+ \frac{\partial}{\partial x}(k\frac{\partial T}{\partial x}) + \frac{\partial}{\partial y}(k\frac{\partial T}{\partial y}) + \frac{\partial}{\partial z}(k\frac{\partial T}{\partial z})]dxdydz

物质体微元能量变化率

微元的总能量包括动能和内能两部分，所以

A=ρDDt(e^+U22)dxdydzA = \rho\frac{D}{Dt}(\hat e + \frac{U^2}{2})dxdydz

分量形式

A=B+CA = B + C

即

ρDDt(e^+U22)=ρq˙+∂∂x(k∂T∂x)+∂∂y(k∂T∂y)+∂∂z(k∂T∂z)−(∂(up)∂x+∂(vp)∂y+∂(wp)∂z)+∂(uτxx)∂x+∂(uτyx)∂y+∂(uτzx)∂z+(∂(up)∂x+∂(vp)∂y+∂(wp)∂z)+∂(uτxx)∂x+∂(uτyx)∂y+∂(uτzx)∂z+∂(vτxy)∂x+∂(vτyy)∂y+∂(vτzy)∂z+∂(wτxz)∂x+∂(wτyz)∂y+∂(wτzz)∂z+ρf⃗⋅U\begin{aligned} \rho\frac{D}{Dt}(\hat e &+ \frac{U^2}{2}) = \rho \dot q+ \frac{\partial}{\partial x}(k\frac{\partial T}{\partial x}) + \frac{\partial}{\partial y}(k\frac{\partial T}{\partial y}) + \frac{\partial}{\partial z}(k\frac{\partial T}{\partial z}) \\ &-(\frac{\partial(up)}{\partial x}+\frac{\partial(vp)}{\partial y}+\frac{\partial(wp)}{\partial z})+\frac{\partial(u\tau_{xx})}{\partial x} + \frac{\partial(u\tau_{yx})}{\partial y} + \frac{\partial(u\tau_{zx})}{\partial z} \\ &+(\frac{\partial(up)}{\partial x}+\frac{\partial(vp)}{\partial y}+\frac{\partial(wp)}{\partial z})+\frac{\partial(u\tau_{xx})}{\partial x} + \frac{\partial(u\tau_{yx})}{\partial y} + \frac{\partial(u\tau_{zx})}{\partial z} \\ &+ \frac{\partial(v\tau_{xy})}{\partial x} + \frac{\partial(v\tau_{yy})}{\partial y} + \frac{\partial(v\tau_{zy})}{\partial z} + \frac{\partial(w\tau_{xz})}{\partial x} + \frac{\partial(w\tau_{yz})}{\partial y} + \frac{\partial(w\tau_{zz})}{\partial z} + \rho \vec f\cdot U \end{aligned}

即

ρD(e^+U2/2)Dt=∇⋅(k∇T)−∇⋅(pU)+S⃗\rho\frac{D(\hat e+U^2/2)}{Dt} = \nabla\cdot(k\nabla T) -\nabla\cdot(pU) + \vec S

注意，对于流动的物质体微元计算得到的是非守恒型方程。

由动量方程 x 方向的受力分析式

ρDuDt=−∂p∂x+∂τxx∂x+∂τyx∂y+∂τzx∂z+ρfx\rho\frac{Du}{Dt} = -\frac{\partial p}{\partial x} + \frac{\partial\tau_{xx}}{\partial x} + \frac{\partial\tau_{yx}}{\partial y} + \frac{\partial\tau_{zx}}{\partial z} + \rho f_x

代入 u2/2u^2/2 ，可以得到

ρDDt(u22)=−u∂p∂x+u∂τxx∂x+u∂τyx∂y+u∂τzx∂z+ρufx\rho\frac{D}{Dt}(\frac{u^2}{2}) = -u\frac{\partial p}{\partial x} + u\frac{\partial\tau_{xx}}{\partial x} + u\frac{\partial\tau_{yx}}{\partial y} + u\frac{\partial\tau_{zx}}{\partial z} + \rho uf_x

而

ρDDt(U22)=ρDDt(u22+v22+w22)\rho\frac{D}{Dt}(\frac{U^2}{2}) = \rho\frac{D}{Dt}(\frac{u^2}{2} + \frac{v^2}{2} + \frac{w^2}{2})

从能量方程中减去所有方向的动能项，可以得到只有内能的能量方程

ρDe^Dt=ρq˙+∂∂x(k∂T∂x)+∂∂y(k∂T∂y)+∂∂z(k∂T∂z)−p(∂(u)∂x+∂(v)∂y+∂(w)∂z)+τxx∂u∂x+τyx∂u∂y+τzx∂u∂z+τxy∂v∂x+τyy∂v∂y+τzy∂v∂z+τxz∂w∂x+τyz∂w∂y+τzz∂w∂z\begin{aligned} \rho\frac{D\hat e}{Dt} &= \rho \dot q+ \frac{\partial}{\partial x}(k\frac{\partial T}{\partial x}) + \frac{\partial}{\partial y}(k\frac{\partial T}{\partial y}) + \frac{\partial}{\partial z}(k\frac{\partial T}{\partial z}) -p(\frac{\partial(u)}{\partial x}+\frac{\partial(v)}{\partial y}+\frac{\partial(w)}{\partial z}) \\ &+ \tau_{xx}\frac{\partial u}{\partial x} + \tau_{yx}\frac{\partial u }{\partial y} + \tau_{zx}\frac{\partial u }{\partial z} + \tau_{xy}\frac{\partial v }{\partial x} + \tau_{yy}\frac{\partial v }{\partial y} + \tau_{zy}\frac{\partial v }{\partial z} + \tau_{xz}\frac{\partial w }{\partial x} + \tau_{yz}\frac{\partial w }{\partial y} + \tau_{zz}\frac{\partial w }{\partial z} \end{aligned}

注意，这个方程没有体积力，应力拿出了速度梯度之外，而且它是非守恒形式。

利用下面的切应力对称性，上式可以进一步改写。

τij=τji\tau_{ij} = \tau_{ji}

利用下面流体物性关系，上式进一步可以改写成完全流场变量表示的能量方程。

∇⋅τ=∇⋅[μ(∇V⃗+(∇V⃗)T)]+∇(λ∇⋅V⃗)\nabla\cdot \tau = \nabla\cdot[\mu (\nabla\vec V + (\nabla\vec V)^T)] + \nabla(\lambda\nabla\cdot\vec V)

守恒型

根据散度展开 ，可以利用守恒转换将上面非守恒型方程改成守恒型方程。

∂∂tρe+∇⋅(ρUe)=∇⋅(k∇T)−∇⋅(pU)+S⃗\frac{\partial}{\partial t}\rho e + \nabla\cdot (\rho U e)= \nabla\cdot(k\nabla T) -\nabla\cdot(pU) + \vec S

e=e^+U22e = \hat e + \frac{U^2}{2}

张量表达

物质体的能量为

E=m(e^+12U2)E = m(\hat e + \frac{1}{2}U^2)

根据热力学第一定律，

能量的变化 = 吸收的热量 - 系统对外做的功

(dEdt)MV=Q−W(\frac{dE}{dt})_{MV} = Q - W

  • QQ 包含两部分
    • 内部产生和消失的 QVQ_V

    • QV=∫Vq˙VdVQ_V = \int_V \dot q_V dV

    • 增加为正，减少为负。此处为正，即热量产生。
    • 通过表面输运的 QSQ_S

    • QS=−∫Sq˙S⋅n⃗dS=−∫V∇⋅q˙SdVQ_S = -\int_S \dot q_S\cdot \vec n dS = -\int_V \nabla\cdot \dot q_S dV

    • 沿着面法向向外为正，向内为负。此处负号表示热量流入物质体，即热量增加。
  • WW 包含两部分
    • 体积力做功 WbW_b
    • 表面力做功 WSW_S

    • Wb=−∫V(f⃗b⋅V⃗)dVW_b = -\int_V(\vec f_b \cdot \vec V)dV

体积力做功加负号，就是物质体通过体积力对外做功。

WS=−∫V(f⃗S⋅U)dV=−∫S(Σ⋅U)⋅n⃗dS=−∫V∇⋅(Σ⋅U)dVW_S = -\int_V(\vec f_S\cdot U)dV = -\int_S(\Sigma\cdot U)\cdot\vec ndS = -\int_V\nabla\cdot(\Sigma\cdot U)dV

面积力沿着法向向外为正，向内为负。面积力做功加负号，就是物质体通过面积力对外做功。
利用动量方程中对表面力的讨论，得到

WS=−∫V∇⋅[(−pI⃗+τ)⋅U]dVW_S =-\int_V\nabla\cdot[(-p\vec I + \tau)\cdot U]dV

利用张量计算法则，得到

WS=−∫V[−∇⋅(pU)+∇⋅(τ⋅U)]dVW_S =-\int_V [-\nabla\cdot(p U) + \nabla\cdot(\tau\cdot U)]dV

代入能量方程为

(dEdt)MV=∫V[∂∂t(ρe)+∇⋅(ρUe)]dV=(\frac{dE}{dt})_{MV} = \int_V[\frac{\partial}{\partial t}(\rho e) + \nabla\cdot(\rho U e)]dV =

∫Vq˙VdV−∫V∇⋅q˙SdV+∫V[−∇⋅(pU)+∇⋅(τ⋅U)]dV+∫V(f⃗b⋅U)dV\int_V \dot q_V dV-\int_V \nabla\cdot \dot q_S dV + \int_V [-\nabla\cdot(pU) + \nabla\cdot(\tau\cdot U)]dV + \int_V(\vec f_b \cdot U)dV

拿去相同的积分，得到完整的能量方程

∂∂t(ρe)+∇⋅(ρUe)=−∇⋅q˙S−∇⋅(pU)+∇⋅(τ⋅U)+f⃗b⋅U+qV\frac{\partial}{\partial t}(\rho e) + \nabla\cdot(\rho U e) = -\nabla\cdot \dot q_S -\nabla\cdot(pU) + \nabla\cdot(\tau\cdot U) + \vec f_b \cdot U + q_V

因具体问题会有其他更加复杂的形式，为了保证理解，本阶段不用深入。不用担心，以后遇到会在合适的时候继续讨论。

这里直接给出温度相关的能量方程为

∂∂t(ρcpT)+∇⋅(ρcpUT)=∇⋅(k∇T)+QT\frac{\partial}{\partial t}(\rho c_pT) + \nabla\cdot(\rho c_p U T) = \nabla\cdot(k\nabla T) + Q^T

通用方程

通用推导

通过上面的讨论，可以看到无论是什么物理量总是有雷诺输运定理

change of BB over time Δt\Delta t within the material volume (MV)

==

surface flux of BB over time Δt\Delta t across the control volume

++

source/sink of BB over time Δt\Delta t within control volume

物质体的物理量变化 = 经过控制体表面的通量变化 + 控制体内部的产生/消失

  1. 第一项

根据雷诺输运定理，

ddt(∫MV(ρϕ)dV)=∫V[∂∂t(ρϕ)+∇⋅(ρUϕ)]dV\frac{d}{dt}(\int_{MV}(\rho\phi)dV) = \int_V[\frac{\partial}{\partial t}(\rho\phi) + \nabla\cdot(\rho U\phi)]dV

结合前面对速度散度的两次讨论以及雷诺输运定义的讨论，我们可以理解 ρUϕ\rho U\phi 表示流动中物理量 ϕ\phi 的输运，称为对流通量 (convective flux)。

我们定义

Fcϕ=ρUϕF^{\phi}_c = \rho U \phi

  1. 第二项

同样的，我们定义扩散通量 (diffusion flux)

Fdϕ=−Γϕ∇ϕF^{\phi}_d = -\Gamma^{\phi}\nabla\phi

termII=−∫SFdϕ⋅n⃗dS=−∫V∇⋅FdϕdV=∫V∇⋅(Γϕ∇ϕ)dVtermII = -\int_S F^{\phi}_{d}\cdot \vec ndS = -\int_V \nabla\cdot F^{\phi}_{d}dV = \int_V\nabla\cdot(\Gamma^{\phi}\nabla\phi)dV

负号是因为扩散的本质是系统的“损耗”。

  1. 第三项

称为源项，写成

termIII=∫VSϕdVtermIII = \int_V S_{\phi}dV

最终，

通用方程为：

∫V[∂∂t(ρϕ)+∇⋅(ρϕU)]dV−∫V∇⋅(Γϕ∇ϕ)dV=∫VSϕdV\int_V[\frac{\partial}{\partial t}(\rho\phi) + \nabla\cdot(\rho\phi U)]dV - \int_V\nabla\cdot(\Gamma^{\phi}\nabla\phi)dV = \int_V S_{\phi}dV

补充讨论

基于前文对雷诺输运定理的讨论，我们停下脚步考虑一下输运过程中的物理本质。

对于我们所研究的流体来说，因为对流、扩散的物理现象，总是应该有以下的守恒关系

控制体的物理量的增加（正号）
==
因对流机制通过控制体边界的物理量流入（与控制体表面方向相反，负号）
++
因扩散机制通过控制体边界的物理量流出（与控制体表面方向相同，正号）
++
因产生源的物理量变化（正号）

所以，我们就可以理解，守恒方程总结为

∂∂t(ρϕ)=−∇⋅(ρϕU)+∇⋅(Γϕ∇ϕ)+Sϕ\frac{\partial}{\partial t}(\rho\phi) = -\nabla\cdot(\rho\phi U)+ \nabla\cdot(\Gamma^{\phi}\nabla\phi) + S_{\phi}

这个表达式的四大项就对应了物理本质的四大项。

归纳方程

对比之前分别推导出的 N-S 方程

  1. 质量方程

∂∂tρ+∇⋅(ρU)=0\frac{\partial}{\partial t}\rho + \nabla\cdot(\rho U) = 0

  1. 动量方程

∂∂t(ρU)+∇⋅(ρUU)=∇⋅(μ∇U)−∇p+Q⃗V\frac{\partial}{\partial t}(\rho U) + \nabla \cdot (\rho UU) = \nabla\cdot(\mu\nabla U)-\nabla p + \vec Q_V

  1. 能量方程

∂∂t(ρcpT)+∇⋅(ρcpUT)=∇⋅(k∇T)+QT\frac{\partial}{\partial t}(\rho c_pT) + \nabla\cdot(\rho c_p U T) = \nabla\cdot(k\nabla T) + Q^T

总结有通用形式基本方程

∂∂t(ρϕ)+∇⋅(ρUϕ)=∇⋅(Γ∇ϕ)+Sϕ\frac{\partial}{\partial t}(\rho \phi) + \nabla \cdot (\rho U\phi) = \nabla\cdot(\Gamma\nabla\phi) + S_{\phi}

从左至右，我们依次称为：时间项、对流项、扩散项、源项。

小结

到此为止，流体力学的基本方程已经大体讨论结束。

希望读者能快速的跨过计算流体力学的这第一道坎。