CFD理论基础01 数值计算初步和有限差分

参考：

Computational fluid dynamics : the basics with applications in SearchWorks catalog (stanford.edu)

Numerical Methods for Partial Differential Equations | ScienceDirect

The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM® and Matlab | SpringerLink

GitHub - surajp92/CFD_Julia: This repository contains fundamental codes related to CFD that can be included in any graduate level CFD coursework.

此篇讨论基于有限差分法直观的阐述数值求解思路，对有限差分法有了解的可以直接跳过此篇。

我们有流体力学基本方程的通用形式如下

$\frac{\partial}{\partial t}(\rho \phi) + \nabla \cdot (\rho U\phi) = \nabla\cdot(\Gamma\nabla\phi) + S_{\phi}$

方程中包含了不同的偏导项，偏导项在数值计算中怎么处理呢？

有限差分法是最直观的偏微分方程的数值求解方法。虽然目前很多的流体计算方法是基于有限体积法开发的，但是有限体积法中的离散格式也会涉及到基于有限差分的离散格式。

所以，有限差分思想很重要。我们从数值计算思路出发，了解有限差分法的基本格式，具体到偏微分方程的数值计算思路，掌握有限差分思想。

数值计算思路

对于某一类类似的物理现象，科学家总是能找出其中的物理规律，建立物理模型。然后使用数学工具分析，得到描述该物理现象的一个或者一组数学方程（常微分方程 ODE 或偏微分方程 PDE），也就是使用数学方程来描述某个物理场在空间和时间中的连续变化情况。这类方程大多过于复杂而难以直接解析求解，比如复杂的常微分方程组和偏微分方程组。

科学家提出对连续数学方程的数值求解方法，也就是建立对求解空间和时间的有限离散，也就是使用有限数量的空间节点和时间节点代替连续的物理区域和时间区间。每个离散点上都可以通过某些数学方法求得数值。当离散点无穷多的时候，计算得到各个离散点上的物理量可以近似认为是连续的，也就是得到了整个连续物理场，也就是近似求得了原数学方程的数值解。不过，离散点总归是有限的，使用有限的离散点去近似代替连续的时空物理量场总是有误差的。当误差能满足科研或者生产要求时，我们认为数值求解结果是正确的，可以指导科研和生产。

一般来说，数值方法的通用思路如下：

微分方程
↓
（有限差分法或有限体积法等）
↓
离散方程
↓
（矩阵组装）
↓
线性代数求解
↓
数值解

怎么去离散连续的数学方程呢？下面通过有限差分法详细介绍数值计算。

差分格式

|275

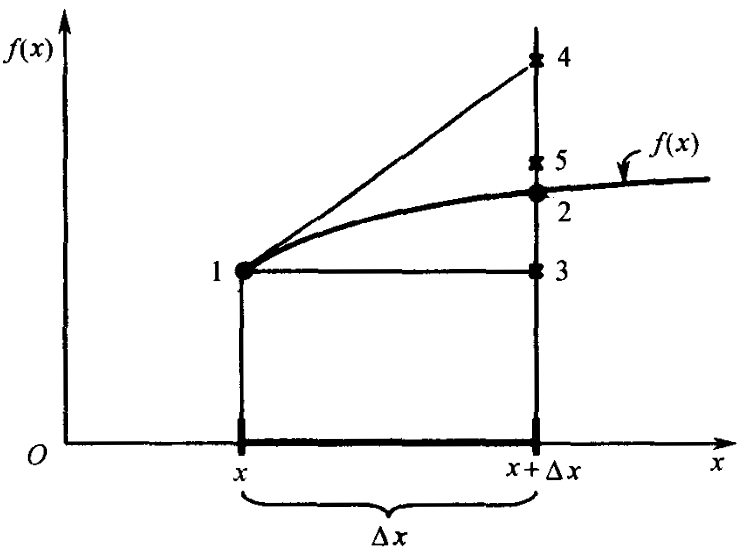
如上图所示，有连续方程方程 $f(x)$ ，该连续函数在 $x+\Delta x$ 处的准确值应该是点 2 处的函数值。怎么去求点 2 的函数值呢？

对 $x$ 的连续函数 $f(x)$ 作泰勒展开，有

$f(x+\Delta x)=f(x)+\frac{\partial f}{\partial x}\Delta x+\frac{\partial^2f}{\partial x^2}\frac{(\Delta x)^2}{2} + ...$

我们可以对物理量 $\phi$ 进行以下的泰勒展开

$\phi_{i+1,j} = \phi_{i,j} + (\frac{\partial\phi}{\partial x})_{i,j}\Delta x + (\frac{\partial^2\phi}{\partial x^2})_{i,j}\frac{(\Delta x)^2}{2} + (\frac{\partial^3\phi}{\partial x^3})_{i,j}\frac{(\Delta x)^3}{6}+...\tag{1}$

$\phi_{i-1,j} = \phi_{i,j} - (\frac{\partial\phi}{\partial x})_{i,j}\Delta x + (\frac{\partial^2\phi}{\partial x^2})_{i,j}\frac{(\Delta x)^2}{2} - (\frac{\partial^3\phi}{\partial x^3})_{i,j}\frac{(\Delta x)^3}{6}+...\tag{2}$

注意展开式（1）和（2）都带了省略号，即两边严格相等，没有近似处理。

式（1）移项，整理得到一阶偏导数的一阶向前差分（前项 - 本项）

$(\frac{\partial\phi}{\partial x})_{i,j} = \frac{\phi_{i+1,j}-\phi_{i,j}}{\Delta x} + O(\Delta x) \tag{3}$

式（2）移项，整理得到一阶偏导数的一阶向后差分（本项 - 后项）

$(\frac{\partial\phi}{\partial x})_{i,j} = \frac{\phi_{i,j}-\phi_{i-1,j}}{\Delta x} + O(\Delta x) \tag{4}$

式（1）减去式（2）得到一阶偏导数的二阶中心差分

$(\frac{\partial\phi}{\partial x})_{i,j} =\frac{\phi_{i+1,j}-\phi_{i-1,j}}{2\Delta x} + O(\Delta x)^2 \tag{5}$

式（1）加上式（2）得到二阶偏导数的二阶中心差分

$(\frac{\partial^2\phi}{\partial x^2})_{i,j} = \frac{\phi_{i+1,j}-2\phi_{i,j} + \phi_{i-1,j}}{2\Delta x} + O(\Delta x)^2 \tag{6}$

式（3）（4）（5）（6）带有高阶项，所以两边也是严格相等，没有近似处理。

对于混合偏导数，可以对一阶偏微分作以下的泰勒展开

$(\frac{\partial\phi}{\partial y})_{i+1,j} = (\frac{\partial\phi}{\partial y})_{i,j} + (\frac{\partial^2\phi}{\partial x\partial y})_{i,j}\Delta x + (\frac{\partial^3\phi}{\partial x^2\partial y})_{i,j}\frac{(\Delta x)^2}{2} + (\frac{\partial^4\phi}{\partial x^3\partial y})_{i,j}\frac{(\Delta x)^3}{6} + ...$

$(\frac{\partial\phi}{\partial y})_{i-1,j} = (\frac{\partial\phi}{\partial y})_{i,j} - (\frac{\partial^2\phi}{\partial x\partial y})_{i,j}\Delta x + (\frac{\partial^3\phi}{\partial x^2\partial y})_{i,j}\frac{(\Delta x)^2}{2} + (\frac{\partial^4\phi}{\partial x^3\partial y})_{i,j}\frac{(\Delta x)^3}{6} + ...$

上面第一式减去第二式得到

$(\frac{\partial^2\phi}{\partial x\partial y})_{i,j} = \frac{(\frac{\partial\phi}{\partial y})_{i+1,j}-(\frac{\partial\phi}{\partial y})_{i-1,j}}{2\Delta x} + (\frac{\partial^4\phi}{\partial x^3\partial y})_{i,j}\frac{(\Delta x)^2}{12} +...$

偏导项替换为下面的一阶偏微分的二阶中心差分格式（保持精度一致）（仅对 y 方向）

$(\frac{\partial\phi}{\partial y})_{i+1,j} = \frac{\phi_{i+1,j+1}-\phi_{i+1,j-1}}{2\Delta y} + O(\Delta y)^2$

$(\frac{\partial\phi}{\partial y})_{i-1,j} =\frac{\phi_{i-1,j+1}-\phi_{i-1,j-1}}{2\Delta y} + O(\Delta y)^2$

有

$(\frac{\partial^2\phi}{\partial x\partial y})_{i,j} =\frac{\phi_{i+1,j+1}-\phi_{i+1,j-1}-\phi_{i-1,j+1}+\phi_{i-1,j-1}}{4\Delta x\Delta y} + O[(\Delta x)^2,(\Delta y)^2] \tag{7}$

当然，我们还可以构造推导出更多形式更高精度的差分格式。对于常见的大多数的 CFD 计算，偏导处理到二阶精度已经足够。在实际的数值计算中，我们可以省略高阶项，将偏导项替换成线性代数项，从而进行后续计算。

多项式构造差分

我们通过边界的处理，来简单介绍一些差分格式的多项式构造方法。

|225

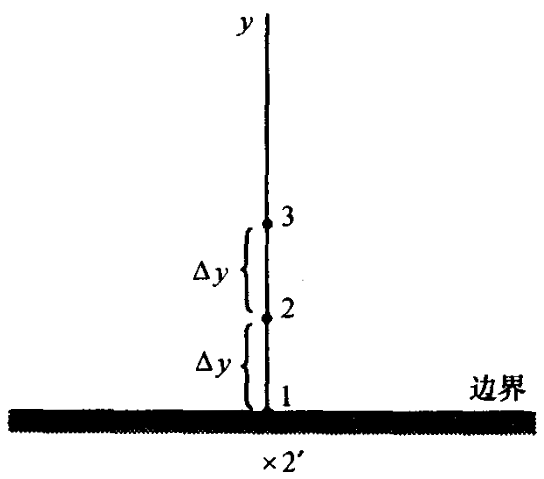
对于上图这种情况，边界点 1 上可以构造一阶精度的差分格式

$(\frac{\partial \phi}{\partial y})_1 = \frac{\phi_2-\phi_1}{\Delta y} + O(\Delta y)$

但是想构造二阶精度差分格式就比较困难，因为边界上缺失一侧的构造点。

例如

$\cancel{(\frac{\partial \phi}{\partial y})_1 = \frac{\phi_2 - \phi_2^{'}}{2\Delta y} + O(\Delta y)^2}$

我们在边界上可以通过多项式构造高精度的差分格式

假设物理量 $\phi$ 在这么一段微小离散尺度上是连续的，那么可以用多项式描述

$\phi = a + by + cy^2 \tag{8}$

那么，在图上 1 点，有 $y = 0$

$\phi_1 = a$

在图上 2 点， $y = \Delta y$

$\phi_2 = a + b\Delta y + c(\Delta y)^2$

在图上 3 点， $y = 2\Delta y$

$\phi_2 = a + b(2\Delta y) + c(2\Delta y)^2$

由这三点可以求解得到 $b$

$b = \frac{-3\phi_1 + 4\phi_2-\phi_3}{2\Delta y}$

在对式（8）求 y 偏导

$\frac{\partial\phi}{\partial y}=b + 2cy$

在边界处， $y = 0$

$(\frac{\partial\phi}{\partial y})_1=b$

得到单侧差分格式（和泰勒展开的项进行对比，可以知道此表达式的精度为二阶精度）

$(\frac{\partial\phi}{\partial y})_1=\frac{-3\phi_1 + 4\phi_2-\phi_3}{2\Delta y}+O(\Delta y)^2$

类似的，我们可以使用多项式方法构造使用更多点信息的更高精度差分格式，以保证边界上计算准确。

差分格式具体怎么用在偏微分方程的求解上呢？

我们通过简单的问题举例说明。

差分方程的构造

以一维非稳态热传导方程为例（材料总长 L）

$\frac{\partial T}{\partial t}=\alpha\frac{\partial^2T}{\partial x^2}$

左侧为时间项，右侧为扩散项，该方程没有对流项和源项

如果是 Dirichlet 边界条件

$\begin{cases} T(0,t) &= Tr \\ T(L,t) &= Tl \end{cases}$

如果是 Neumann 边界条件

$\begin{cases} \frac{\partial T}{\partial x}(0,t) = T^{'}_r(t) \\ \frac{\partial T}{\partial x}(L,t) = T^{'}_l(t) \end{cases}$

初始条件

$T(x,0) = T_0(x)$

离散

将计算域划分成 $nx$ 个单元，时间步长 $dt$ ，计算时间步 $nt$ 步，所以

每个单元的长度为

$dx = L / nx$

总计算时间为

$tt = dt * nt$

我们采用 C++ 的序号约定，即从 0 开始。

右边界节点 $T_0$ ，

中间节点从右向左依次是

$T_1,T_2,T_3,...,T_{nx-1}$

左边界节点 $T_{nx}$

如果使用上面的 Dirichlet 边界条件，则

$\begin{cases} T_0 = T_r \\ T_{nx} = T_l \end{cases}$

如果使用上面的 Neumann 边界条件，则

显式构造

利用差分格式得到差分方程为

$\frac{T^{n+1}_i-T^{n}_i}{\Delta t}=\alpha\frac{T^{n}_{i+1}-2T^{n}_{i}+T^{n}_{i-1}}{(\Delta x)^2}$

上标 $n$ 为当前时间步，已知量
上标 $n+1$ 为下一时间步，待求未知量
下标 $i$ 为当前点， $i-1$ 为上一点， $i+1$ 为下一点

整理后可得

$T^{n+1}_i=T^{n}_i+\alpha\frac{\Delta t}{(\Delta x)^2}(T^{n}_{i+1}-2T^{n}_{i}+T^{n}_{i-1})$

方程左边为待求未知量，右侧为已知量。

这种类型的表达式可以直接迭代求解。即显式的按时间推进求解，通过每一个时间步的旧值可以算出下一个时间步的新值。

隐式构造

如果我们处理差分方程得到如下形式

$\frac{T^{n+1}_i-T^{n}_i}{\Delta t}=\alpha\frac{\frac{T^{n+1}_{i+1}+T^{n}_{i+1}}{2}-2(\frac{T^{n+1}_{i}+T^{n}_{i}}{2})+\frac{T^{n+1}_{i-1}+T^{n}_{i-1}}{2}}{(\Delta x)^2}$

这种引入新时间步与旧时间步之间平均值的格式被称为克兰克 - 尼科尔森格式。这种格式下，新时间步的未知量不止是 $T^{n+1}_i$ ，而且还有 $T^{n+1}_{i+1}$ 和 $T^{n+1}_{i-1}$ 。

整理上式有

$\begin{aligned} \frac{\alpha\Delta t}{2(\Delta x)^2}T^{n+1}_{i-1} &- \bigg[1 + \frac{\alpha\Delta t}{(\Delta x)^2}\bigg]T_i^{n+1} + \frac{\alpha\Delta t}{2(\Delta x)^2}T_{i+1}^{n+1} \\ &= -T_i^n - \frac{\alpha\Delta t}{2(\Delta x)^2}(T_{i+1}^{n} - 2T_i^n + T_{i-1}^n) \end{aligned}$