参考：

我们有流体力学基本方程的通用形式如下

∂∂t(ρϕ)+∇⋅(ρUϕ)−∇⋅(Γ∇ϕ)=Sϕ\frac{\partial}{\partial t}(\rho \phi) + \nabla \cdot (\rho U\phi) - \nabla\cdot(\Gamma\nabla\phi) = S_{\phi}

注意！这里的 ϕ\phi 仅表示某种物理量，不要和以后会经常出现的质量通量混淆！

从左至右依次为时间项、对流项、扩散项、源项。其中 Γ\Gamma 是扩散系数。

本阶段推荐优先理解四大项的离散，把握有限体积法的主要思想，以后再分别理解网格、边界条件、高级离散格式等 内容。

有限体积法的重点

  • 网格单元信息存储在体心上
  • 方程对网格单元做体积分

下面详细介绍。

半离散方程

在某一个时间步上，把基本方程对空间离散的单元（网格单元）上做体积积分，有

∫VP(∂∂t(ρϕ)+∇⋅(ρUϕ)−∇⋅(Γ∇ϕ))dV=∫VPSϕdV\int_{V_P}\bigg(\frac{\partial}{\partial t}(\rho \phi) + \nabla \cdot (\rho U\phi) - \nabla\cdot(\Gamma\nabla\phi) \bigg)dV =\int_{V_P} S_{\phi}dV

整理为

∫VP(∂∂t(ρϕ))dV+∫VP(∇⋅(ρUϕ))dV−∫VP(∇⋅(Γ∇ϕ))dV=∫VPSϕdV\begin{aligned} \int_{V_P}\bigg(\frac{\partial}{\partial t}(\rho \phi)\bigg)dV + \int_{V_P}\bigg(\nabla \cdot (\rho U\phi)\bigg)dV - \int_{V_P}\bigg(\nabla\cdot(\Gamma\nabla\phi)\bigg)dV = \int_{V_P} S_{\phi}dV \end{aligned}

说明

正式开始之前，有必要进行一些说明

符号约定

计算流体力学的几乎每本书的符号系统都不太一样，有时候会让人很困惑。

约定后文中

  • 上标指示时间
    • 上标 tt 表示当前时间步（已知量）。
    • 上标 t+1t+1 表示新时间步（待求量）。
    • 更高时间步依次类推，使用上标 t+nt+n。
  • 下标指示空间
    • 下标 PP 表示当前单元体心值（取Owner的 O 实在很容易混淆）。
    • 下标 NN 表示相邻单元体心值（Neighbour）。
    • 下标 ff 表示当前单元和相邻单元之间的界面的面心值（face）。
  • 网格单元属性
    • VPV_P 表示单元的体积。做了体积分后，也就是被积系统的体积。
    • ∂VP\partial V_P 表示单元的总面积。做了面积分后，也就是被积系统的面积。

平均值

对于有限体积法，我们约定单元信息存储在单元的体中心上，近似等于单元的体平均值

ϕP=ϕˉ=1VP∫VPϕ(x)dV\phi_P = \bar \phi = \frac{1}{V_P}\int_{V_P}\phi(x)dV

两个单元的界面上面心值，近似等于面平均值

ϕf=ϕˉf=1Sf∫fϕ(x)dS\phi_f = \bar\phi_f = \frac{1}{S_f}\int_f\phi(x)dS

高斯定理

高斯定理（散度定理，物理量散度在系统的体积积分等于物理量在系统的面积分）

矢量的高斯定理，结果是标量

∫V∇⋅a⃗dV=∫∂Va⃗⋅dS⃗\int_V\nabla \cdot \vec a dV = \int_{\partial V}\vec a\cdot d\vec S

标量的高斯定理，结果是矢量

∫V∇ϕdV=∫∂Vϕ⋅dS⃗\int_V\nabla\phi dV= \int_{\partial V}\phi \cdot d\vec S

时间项

时间项如下，

∫VP(∂∂t(ρϕ))dVdt\int_{V_P}\bigg(\frac{\partial}{\partial t}(\rho \phi)\bigg)dVdt

对时间的偏导和体积没有任何关系，所以上式

∫VP(∂∂t(ρϕ))dVdt=∂∂t(ρϕ)∫VPdV=VP∂∂t(ρϕ)\int_{V_P}\bigg(\frac{\partial}{\partial t}(\rho \phi)\bigg)dVdt = \frac{\partial}{\partial t}(\rho \phi)\int_{V_P}dV = V_P\frac{\partial}{\partial t}(\rho \phi)

最终有

时间项半离散表达式

∫VP(∂∂t(ρϕ))dV=VP∂(ρϕ)∂t\int_{V_P}\bigg(\frac{\partial}{\partial t}(\rho \phi)\bigg)dV=V_P\frac{\partial (\rho\phi)}{\partial t}

注意，时间的偏导需要进一步离散处理。

对流项

对流项如下

∫VP(∇⋅(ρUϕ))dV\int_{V_P}\bigg(\nabla \cdot (\rho U\phi)\bigg)dV

由散度定理

∫VP(∇⋅(ρUϕ))dV=∫∂VP(ρUϕ)⋅dS⃗\int_{V_P}\bigg(\nabla \cdot (\rho U\phi)\bigg)dV = \int_{\partial V_P}(\rho U \phi)\cdot d\vec S

单元上的面积分等于各个离散面积分的总和

∫∂VP(ρUϕ)⋅dS⃗=∑f∫∂VP(ρUϕ)f⋅dS⃗\int_{\partial V_P}(\rho U \phi)\cdot d\vec S = \sum_f\int_{\partial V_P}(\rho U\phi)_f\cdot d\vec S

每个离散面上的积分近似（产生误差）等于其面心值乘以面矢量

∑f∫∂VP(ρUϕ)⋅dS⃗≈∑f(ρUϕ)f⋅S⃗f=∑fFfϕf\sum_f\int_{\partial V_P}(\rho U\phi)\cdot d\vec S \approx \sum_f(\rho U\phi)_f\cdot \vec S_f = \sum_fF_f\phi_f

最终有

对流项半离散表达式

∫VP(∇⋅(ρUϕ))dV=∑fFfϕf\int_{V_P}\bigg(\nabla \cdot (\rho U\phi)\bigg)dV = \sum_fF_f\phi_f

其中 FfF_f 被称为质量通量

Ff=ρfUf⋅S⃗fF_f = \rho_fU_f\cdot \vec S_f

定义对流通量有

FluxC=FfϕfFlux^C = F_f\phi_f

理解为因为对流现象，物理量在面上的输运。

注意，因为物理量存储在单元体心上，所以面上的值（下标ff） 需要根据体心值进一步离散处理。

扩散项

扩散项如下

∫VP(∇⋅(Γ∇ϕ))dV\int_{V_P}\bigg(\nabla\cdot(\Gamma\nabla\phi)\bigg)dV

由散度定理

∫VP(∇⋅(Γ∇ϕ))dV=∫∂VP(Γ∇ϕ)⋅dS⃗\int_{V_P}\bigg(\nabla\cdot(\Gamma\nabla\phi)\bigg)dV = \int_{\partial V_P}(\Gamma\nabla\phi)\cdot d\vec S

单元表面是一个完整的闭合面，由若干离散面组成。例如六面体网格由六个离散面组成，单元上的面积分等于这六个个离散面的积分的总和。这里没有引入近似。

∫∂VP(Γ∇ϕ)⋅dS⃗=∑f∫f(Γ∇ϕ)⋅dS⃗\int_{\partial V_P}(\Gamma\nabla\phi)\cdot d\vec S = \sum_f\int_f(\Gamma\nabla\phi)\cdot d\vec S

每个离散面上的积分近似（产生误差）等于其面心值乘以面矢量（因为面心值有方向）

∑f∫f(Γ∇ϕ)⋅dS⃗≈∑f(Γ∇ϕ)f⋅S⃗f\sum_f\int_f(\Gamma\nabla\phi)\cdot d\vec S \approx \sum_f(\Gamma\nabla \phi)_f\cdot \vec S_f

最终有

扩散项半离散表达式

∫VP(∇⋅(Γ∇ϕ))dV=∑f(Γ∇ϕ)f⋅S⃗f\int_{V_P}\bigg(\nabla\cdot(\Gamma\nabla\phi)\bigg)dV = \sum_f(\Gamma\nabla \phi)_f\cdot \vec S_f

定义扩散通量

FluxD=(Γ∇ϕ)f⋅S⃗fFlux^D = (\Gamma\nabla \phi)_f\cdot \vec S_f

理解为因为扩散现象，物理量在面上的输运。

注意，除了面心值，面心值的梯度也需要进一步离散处理。

源项

源项如下

∫VPSϕdV\int_{V_P} S_{\phi}dV

当源项是线性的时候 Sϕ=Su+SpϕS_\phi = S_u + S_p\phi

最终有

源项离散表达式

∫VPSϕdV=SuVP+SpVPϕP\int_{V_P} S_{\phi}dV = S_uV_P + S_pV_P\phi_P

半离散方程

VP∂(ρϕ)∂t+∑fFfϕf−∑f(Γ∇ϕ)f⋅S⃗f=SuVP+SpVPϕPV_P\frac{\partial (\rho\phi)}{\partial t} + \sum_fF_f\phi_f - \sum_f(\Gamma\nabla \phi)_f\cdot \vec S_f = S_uV_P + S_pV_P\phi_P

  • FfϕfF_f\phi_f 称为对流通量 convective flux
  • (Γ∇ϕ)f⋅S⃗f(\Gamma \nabla \phi)_f\cdot \vec S_f 称为扩散通量 diffusive flux

数值处理

半离散方程中还有很多项需要进一步处理。

面插值

线性面插值

对于面心值 UfU_f ，可以基于本单元和邻单元的体心值，根据一定的插值格式得到

比如

Uf=fxUP+(1−fx)UNU_f = f_xU_P + (1-f_x)U_N

fx=fNPN=Xf−XN∣d∣f_x = \frac{fN}{PN} = \frac{X_f - X_N}{|d|}

物性面插值

对于面心值 Γf\Gamma_f ，如果扩散系数也是连续的，可以按照一般面心值离散处理。

如果材料是复合材料，扩散系数在材料变化处理应有一个突变。

插值公式为

Γf=2ΓPΓNΓP+ΓN\Gamma_f = \frac{2\Gamma_P\Gamma_N}{\Gamma_P + \Gamma_N}

参见 The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM® and Matlab | SpringerLink 第225页。

输运面插值

对流是有明显流向特征的物理现象。对于一个物理量的对流输运来说，下游的物理量总是小于等于上游。

参考 The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM® and Matlab | SpringerLink 第11章。

对于待求的面心上的输运量 ϕf\phi_f 来说，我们需要建立它和体心之间的关系

  1. 如果我们采用线性面插值格式，求解可能会产生振荡（越界）。

  2. 如果我们采用迎风格式ϕf=ϕupwind\phi_f = \phi_{upwind}，求解稳定有界，但是精度低且有扩散性。

  3. 如果我们采用二阶迎风格式，对于强对流，求解会出现大梯度以及振荡（越界）。

  4. 如果我们使用 TVD 格式（以后讨论），求解具有二阶精度且有界。

所以，我们需要知道离散格式对求解有着很大的影响，不用担心，后续会详细讨论这些数值细节。

不管使用哪种格式，最终面心值和体心值建立了某种插值关系。

梯度

回忆 CFD 基本方程中的动量方程，其中可能会出现的压力梯度

∇p\nabla p

要怎么离散呢？

  1. 通过格林高斯法求梯度

对单元面求体积分，应用高斯定理

∫V∇pdV=∫∂VPpdS⃗\int_V \nabla p dV = \int_{\partial V_P}pd\vec S

面积分等于离散面积分之和，离散面的积分继而等于面心值乘以面矢量

∫∂VPpdS⃗=∑fpfSf\int_{\partial V_P}pd\vec S = \sum_f p_fS_f

此外，压力梯度本身和体积没有关系，所以另外有

∫V∇pdV=VP∇pP\int_V \nabla p dV = V_P \nabla p_P

所以可以建立等式关系，最后有

∇pP=1VP∑fpfS⃗f\nabla p_P =\frac{1}{V_P}\sum_fp_f\vec S_f

  1. 通过最小二乘法求梯度

参考 The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM® and Matlab | SpringerLink 第11章。

无论通过哪种方式求梯度，最后得到的是体心梯度值，最后还需要应用面插值格式到面心梯度值。

比如，可以使用简单的线性面插值格式

∇pf=fx∇pP+(1−fx)∇pN\nabla p_f = f_x\nabla p_P + (1-f_x)\nabla p_N

fx=fN/PNf_x = fN/PN

正交修正

扩散项的计算中为什么会有正交修正这个问题呢？

扩散通量的计算为

FluxD=(Γ∇ϕ)f⋅S⃗fFlux^D = (\Gamma\nabla \phi)_f\cdot \vec S_f

如果网格是正交的

(Γ∇ϕ)f⋅S⃗f=ΓϕN−ϕP∣PN∣∣S⃗f∣(\Gamma\nabla \phi)_f\cdot \vec S_f = \Gamma \frac{\phi_N-\phi_P}{|PN|}|\vec S_f|

当网格非正交的时候，如下图所示

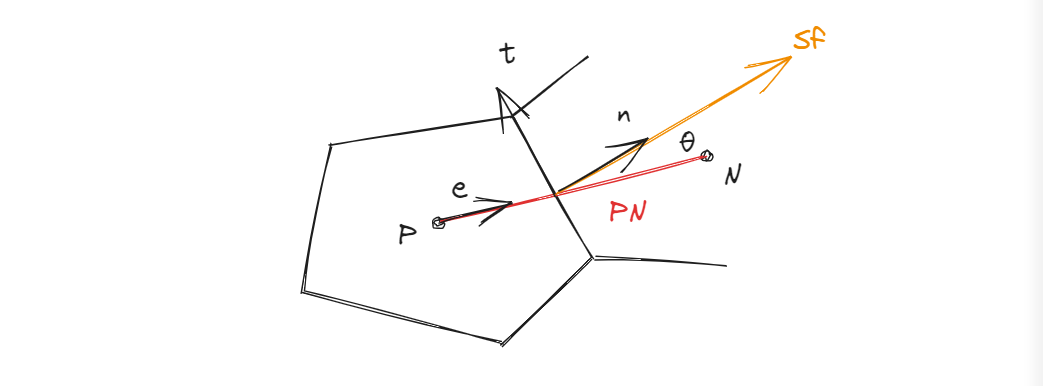
image.png

对于上图面矢量 S⃗f\vec S_f 依然垂直于单元面，但是物理量梯度 ∇ϕf\nabla \phi_f 并不垂直于单元面。

将面矢量 S⃗f\vec S_f 分解成沿 PN 方向 E⃗f\vec E_f 和其他方向分量 T⃗f\vec T_f，T⃗f\vec T_f 的具体方向由正交近似 方法决定。

S⃗f=E⃗f+T⃗f\vec S_f = \vec E_f + \vec T_f

此时扩散通量计算为

(Γ∇ϕ)f⋅S⃗f=(Γ∇ϕ)f⋅E⃗f+(Γ∇ϕ)f⋅T⃗f=(Γ∂ϕ∂n)fEf+(Γ∇ϕ)f⋅T⃗f=ΓϕN−ϕP∣PN∣Ef+(∇ϕ)f⋅T⃗f\begin{aligned} (\Gamma \nabla \phi)_f\cdot\vec S_f &= (\Gamma\nabla \phi)_f\cdot\vec E_f + (\Gamma \nabla \phi)_f\cdot\vec T_f \\ &=(\Gamma\frac{\partial \phi}{\partial n})_fE_f + (\Gamma\nabla \phi)_f\cdot\vec T_f \\ &= \Gamma\frac{\phi_N - \phi_P}{|PN|}E_f + (\nabla \phi)_f\cdot\vec T_f \end{aligned}

右边第一项称为正交影响，第二项称为非正交影响。

正交修正本质上是把扩散量调整到合适的数值，近似分解到了单元面法向上。

  1. 关于非正交贡献

可以通过插值得到界面上的温度梯度

(∇ϕ)f=gN(∇ϕ)P+gP(∇ϕ)N(\nabla \phi)_f = g_N(\nabla \phi)_P + g_P(\nabla \phi)_N

其中，由高斯通量求得体心温度的梯度有

(∇T)P=1VP∑f(Tf⋅S⃗f)(\nabla T)_P = \frac{1}{V_P}\sum_f(T_f\cdot\vec S_f)

最终还是归结在面通量的计算。

  1. 关于正交贡献

常见有以下几种近似处理

  • 最小修正近似
  • 正交修正近似
  • 超松弛近似

如果我们采用正交修正近似，即定义

E⃗f=Sfe⃗\vec E_f = S_f\vec e

参考 The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM® and Matlab | SpringerLink 第241页。

以后会详细讨论。

请考虑一个问题，四大项都需要正交修正吗？（不需要回答，带着问题即可）

其他

其他像是网格扭曲修正、松弛等等数值方法均放在后续详细讨论。本阶段，只需要把握最基本的离散思路即可。

离散方程

半离散方程已经讨论了四大项的离散思路，下面将结合“数值处理”和“时间积分”，得到最后的离散方程。

以动量方程为例

∂U∂t+∇⋅(UU)−∇⋅(ν∇U)=−∇p\frac{\partial U}{\partial t} + \nabla\cdot(UU)-\nabla\cdot(\nu\nabla U) = -\nabla p

时间项

时间上使用欧拉插值格式

∫t∫V∂U∂tdVdt=∫tVP∂(ρϕ)∂tdt=VPΔtUPt+1−UPtΔt=(UPt+1−UPt)VP\begin{aligned} \int_t\int_V\frac{\partial{U}}{\partial{t}}dVdt &=\int_t V_P\frac{\partial (\rho\phi)}{\partial t} dt \\ &= V_P\Delta t\frac{U_P^{t+1} - U_P^{t}}{\Delta t} \\ &= (U_P^{t+1}-U^t_P)V_P \end{aligned}

比如 OpenFOAM 的 fvSchemes 中指定

1
2
3
4
ddtSchemes
{
	default    Euler;
}

梯度项

采用高斯定理，时间上采用全显式，空间上采用线性插值格式

∫t∫V∇pdVdt=∫tVP1VP∑fpfS⃗fdt=Δt∑fpNt+pPt2S⃗f\begin{aligned} \int_t\int_V\nabla p dVdt &=\int_t V_P\frac{1}{V_P}\sum_fp_f\vec S_f dt\\ &= \Delta t\sum_f\frac{p_N^t + p_P^t}{2}\vec S_f \end{aligned}

比如 OpenFOAM 的 fvSchemes 中指定

1
2
3
4
5
gradSchemes
{
	default    Gauss linear;
	grad(p)    Gauss linear;
}

对流项

使用高斯定理（散度定理），时间上采用全隐式，空间上采用线性插值格式（公式给出中心差分作为演示）

∫f∫V∇⋅(UU)dVdt=∫t∑fFfϕfdt=Δt∑fFftUN∗+UP∗2\int_f\int_V\nabla\cdot(UU)dVdt = \int_t \sum_fF_f\phi_f dt= \Delta t \sum_f F^t_f\frac{U^*_N + U_P^*}{2}

比如 OpenFOAM 的 fvSchemes 中指定

1
2
3
4
5
divSchemes
{
	default    none;
	div(phi,U) Gauss linear;
}

扩散项

采用高斯定理（散度定理），时间上采用隐式，空间上采用线性插值格式、无正交修正（默认使用正交网格）

∫t∫V∇⋅(ν∇U)dVdt=Δt∑f(ν∇U∗)f⋅S⃗f\int_t\int_V\nabla\cdot(\nu\nabla U)dVdt = \Delta t \sum_f(\nu\nabla U^*)_f\cdot \vec S_f

其中

(∇U∗)f⋅S⃗f=UN∗−UP∗∣PN∣⋅∣S⃗f∣(\nabla U^*)_f\cdot \vec S_f = \frac{U_N^* - U_P^*}{|PN|}\cdot |\vec S_f|

梯度项计算已经在上一小节被指定。

比如 OpenFOAM 的 fvSchemes 中指定

1
2
3
4
laplacianSchemes
{
	default    Gauss linear;
}

面插值

对于面心值到体心值的插值

比如

Fft=(Uft⋅S⃗f)F^t_f = (U^t_f\cdot\vec{S}_f)

采用线性面插值

Uft=fxUPt+(1−fx)UNtU^t_f = f_xU^t_P + (1-f_x)U^t_N

比如 OpenFOAM 的 fvSchemes 中指定

1
2
3
4
interpolationSchemes
{
	default linear;
}

正交修正

如果网格是非正交的，梯度计算（如压力梯度）需要采用正交修正的方法。

比如 OpenFOAM 的 fvSchemes 中指定

1
2
3
4
snGradSchemes
{
	default    orthogonal;
}

离散方程

最终离散方程为

(UP∗−UPt)ΔtVP+∑fFftUN∗+UP∗2−∑fνUN∗−UP∗∣d⃗∣⋅∣S⃗f∣=−∑fpNt+pPt2S⃗f\frac{(U^*_P-U^t_P)}{\Delta t}V_P + \sum_f F^t_f\frac{U^*_N + U_P^*}{2} - \sum_f\nu\frac{U_N^* - U_P^*}{|\vec d|}\cdot |\vec S_f| = -\sum_f\frac{p_N^t + p_P^t}{2}\vec S_f

整理为

(1Δt+1VP∑fFft2+1VP∑fν∣S⃗f∣∣d⃗∣)UP∗+1VP∑f(Fft2−ν∣S⃗f∣∣d⃗∣)UN∗=1ΔtUPt−1VP∑fpNt+pPt2S⃗f\begin{aligned} (\frac{1}{\Delta t} + \frac{1}{V_P}\sum_f\frac{F_f^t}{2} + \frac{1}{V_P}\sum_f\nu\frac{|\vec S_f|}{|\vec d|})U_P^* &+ \frac{1}{V_P}\sum_f(\frac{F_f^t}{2}-\nu\frac{|\vec S_f|}{|\vec d|})U_N^* \\ &= \frac{1}{\Delta t}U_P^t -\frac{1}{V_P}\sum_f\frac{p_N^t + p_P^t}{2}\vec S_f \end{aligned}

简写成

APUP∗+∑fANUN∗=SPt−1VP∑fpNt+pPt2S⃗fA_PU^*_P + \sum_fA_NU_N^* = S_P^t - \frac{1}{V_P}\sum_f\frac{p_N^t + p_P^t}{2}\vec S_f

左侧是已知系数矩阵和未知待求量，右侧是已知量。

即是线性代数系统

Ax=bAx = b

可以使用不同的数值方法进行求解。

当然这里又涉及到压力项耦合解法，这里不多赘述，暂时只需要把握主要思路就可以。

小结

到此为止，有限体积法求解偏微分方程的基本思路就梳理清楚了。

也就是，我们通过有限体积法离散控制方程，构建线性代数系统，再通过一些数值方法求解，得到物理场。

不用担心，后续会展开讨论其中的数值细节。